ляется по структурной формуле для плоских механизмов, предложенной П.Л.Чебышевым: W = 3 (К – 1) – 2р5 – р4, где К – общее число звеньев в механизме, включая стойку, р5 – число кинематических пар 5-го класса, р4 – число кинематических пар 4-го класса. Заданный механизм состоит из 4-х звеньев: 1 – кривошип АВ, 2 – шатун ВЕ, 3 – коромысло CD, 4 – стойка (корпус). Механизм имеет 4 вращательные кинематические пары 5-го класса – шарниры A, B, C, D. Механизм не имеет кинематических пар 4-го класса. Вычисляем степень подвижности (число степеней свободы) механизма: W = 3 (К – 1) – 2р5 – р4 = 3 . (4 – 1) – 2 . 4 – 0 = 1, что означает, что механизм имеет одно входное звено (кривошип АВ), которому передается вращение от одного двигателя.
3. Определяем скорости
точек механизма. Угловая скорость кривошипа w1 = pn1 / 30 = 3,14 . 149,2 / 30 = 15,62 1/с.
Скорость точки В VB
= = w1lAB = 15,62
. 0,0625 = 0,98
м/с. Решая графически векторное уравнение 
= 
+ 
, получаем
план скоростей (рис. 6б). Скорость VB изображается отрезком pvb = 49 мм. Отсюда масштабный коэффициент плана скоростей kv = VB / pvb = 0,98
/ 49 = 0,02 (м/с)/мм. Измеряем длины отрезков на плане скоростей и вычисляем
скорости: VC = pvc . kv = 46 . 0,02 = = 0,92 м/с, VE = pve . kv = 61. 0,02 = 1,22 м/с, VS1 = pvs1 . kv = 24,5 . 0,02 = = 0,49 м/с,VS2 = pvs2 . kv = 42 . 0,02 = 0,84 м/с, VS3 =pvs3 . kv = 23 . 0,02 = = 0,46 м/с, VCB = bc .
kv = 49 . 0,02 = 0,98 м/с. Угловые скорости
звеньев 2 и 3: w2 = VCB / lBC = 0,98 / 0,21 = 4,67 1/с,
w3 = VC / lCD = 0,92 / 0,1025 = 8,98 1/с.
Определяем ускорения
точек механизма. 
= 
+
. Но 
= 0, т.к. w1=const.
=w12 lAB= 15,622 . 0,0625 = 15,25 м/с2. Решая
графически систему двух векторных уравнений: 
=+
+
и
=
+
,
получаем план ускорений (рис. 6в). Ускорение aB изображается отрезком pab = 61 мм.
20
Масштабный коэффициент плана ускорений
ka = aB / pab = 15,25 / 61 = = 0,25 (м/с2)/мм.
Нормальное ускорение 
= w22 lBC = 4,672 . 0,21 = = 4,58 м/с2 изображается отрезком bn = / ka = 4,58 / 0,25 = 18 мм. Нормальное ускорение 
= w32 lCD = 8,982 . 0,1025 = 8,27 м/с2 изображается
отрезком pam = / ka = 8,27 / 0,25 = 33 мм. Измеряем длины отрезков на плане ускорений и вычисляем ускорения: aC = pac. ka = = 48 . 0,25 = 12 м/с2, aE = pae . ka = 44 .
0,25
= 11 м/с2, aS1
= pas1 . ka = = 30,5 . 0,25 = 7,6 м/с2, aS2 = pas2 . ka = 51 . 0,25 = 12,8 м/с2, aS3 = = pas3 .
ka = 24 . 0,25 = 6 м/с2.
4. Вычисляем массы звеньев:m1 = 5 lAB = 5 . 0,0625 = 0,31 кг,m2 = = 5 . (lBC + lCE) = 5 . (0,21 + 0,105) = 1,58 кг, m3 = 5 lCD = 5 . 0,1025 = 0,51 кг. Силы тяжести: G1 = m1 g = 0,31 . 9,8 = 3 Н, G2 = m2 g = 1,58 . 9,8 = 15,5 Н, G3 = m3 g = 0,51 . 9,8 = 5 Н.
5. Вычисляем силы инерции, действующие на звенья: Fи1 = m1 aS1 = = 0,31 . 7,6 = 2,4 Н, Fи2 = m2 aS2 = 1,58 . 12,8 = 20,2 Н, Fи3 = m3 aS3 = 0,51 . 6 = = 3,1 Н.
6. Силы, действующие на звенья, показаны на рис. 6г. Вычисляем силу полезного сопротивления: FПС = 100G2 = 100 . 15,5 = 1550 Н.
7. Рычаг Н.Е.Жуковского представляет собой жесткую систему, которая совпадает по конфигурации с планом скоростей, повернутым на 90о в любую сторону; он шарнирно закреплен в полюсе pv, к нему приложены силы, действующие на звенья, и уравновешивающая сила FУ (рис. 6е). Условие равновесия рычага: SMpv(Fi) + Mpv(FУ) = 0. Напомним, что момент Mpv(F) силы F относительно полюса pv есть произведение силы F на плечо h, которое равно длине перпендикуляра, опущенного из полюса pv на линию действия силы F, причем если момент вращает рычаг
21
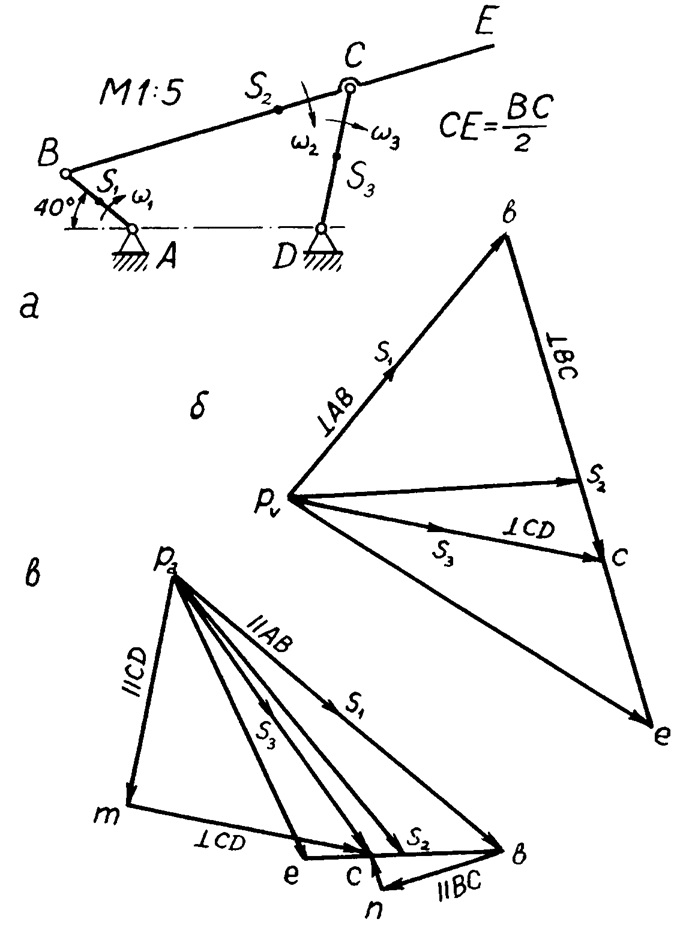
Рис.6: а – кинематическая схема рычажного механизма в заданном положении, б – план скоростей, в – план ускорений.
22
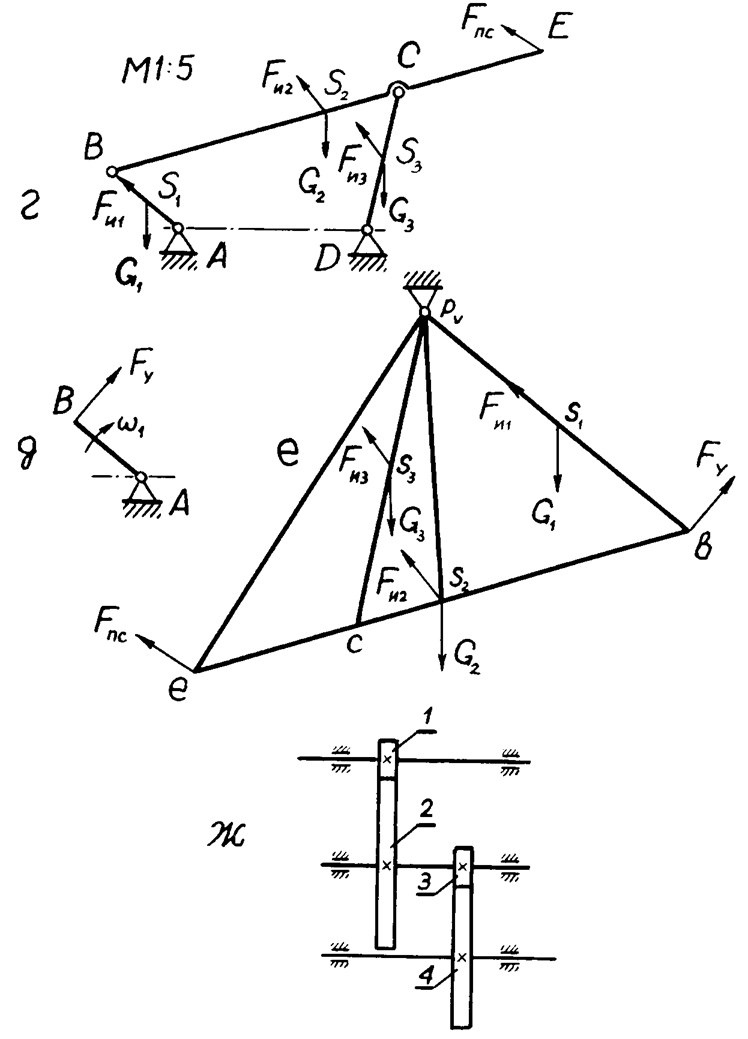
Продолжение рис.6: г – силы, действующие на звенья механизма, д – звено приведения с уравновешивающей силой, е – рычаг Н.Е.Жуковского,
ж – кинематическая схема двухступенчатого редуктора.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.