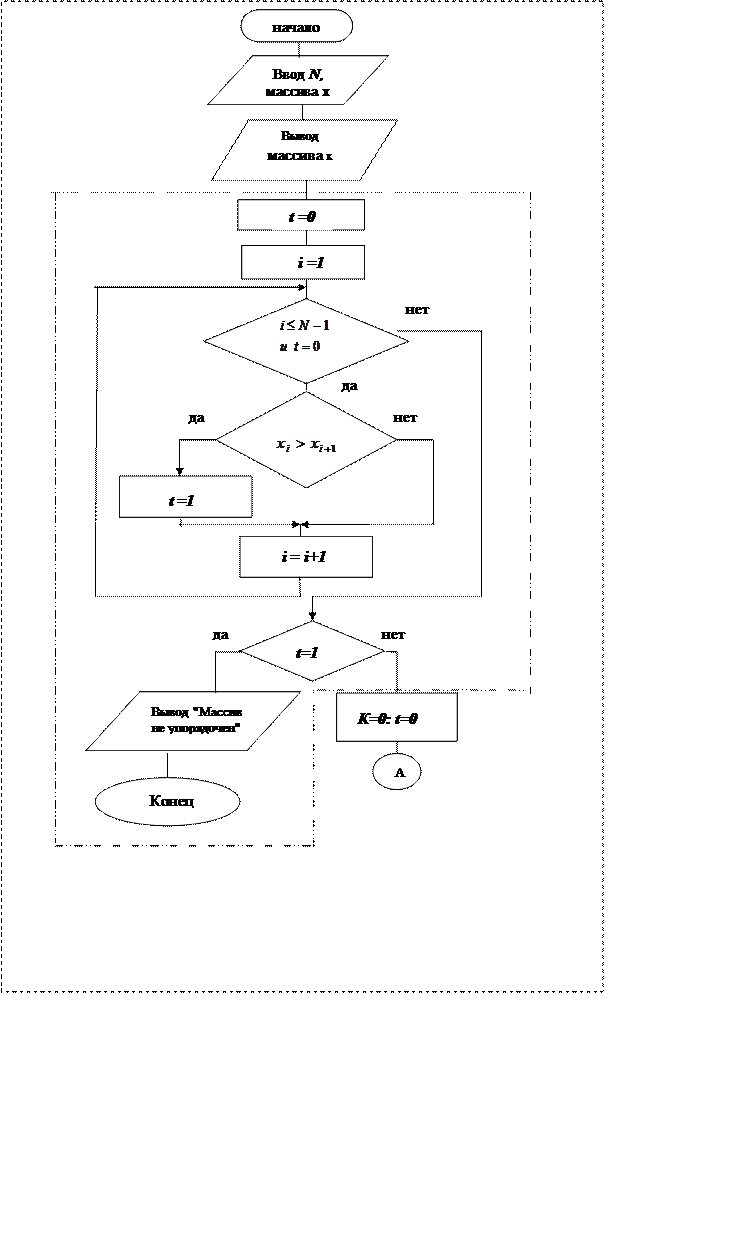
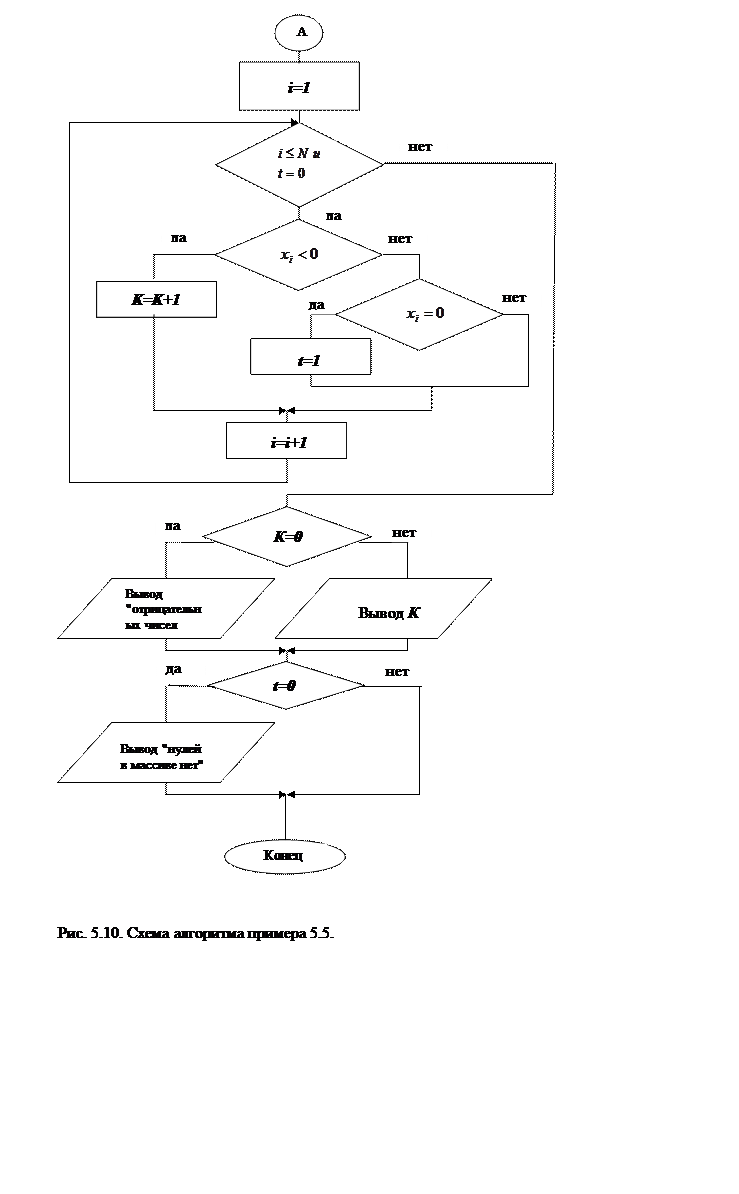
Решение. Поскольку массив упорядочен по не убыванию, а искать в нем нужно только отрицательные числа или нули, то выход из цикла просмотра возможен в двух случаях: когда весь массив просмотрен (т.е. в нем все числа отрицательные), или встретилось значение =0. Введем дополнительную величину t с начальным значением =0, которое изменит его на 1, если встретится элемент =0. Количество найденных отрицательных чисел обозначим через К. Схема алгоритма приведена на рис. 5.10. Она включает в себя проверку введенного массива на упорядоченность по не убыванию (символы, ограниченные пунктиром).
 |
Как уже отмечалось в разделе 5.3., очень часто информация размещается в прямоугольных таблицах, какими представляют себя двумерные массивы (другое название, взятое из математики – матрицы).
Пример двумерного массива Z размерностью 3х4, состоящего из целых чисел, изображен на рисунке.
Элементы такого массива имеют два индекса, первый из
которых означает номер строки, в которой стоит элемент, а второй – номер
столбца.
Например, Z23 означает число =77.
Таким образом, чтобы выбрать нужное число из такого массива нужно задать значения двух его индексов.
Обработка таких массивов осуществляется с использованием циклов. Но в этом случае циклов нужно 2: один – по изменению номера строки, а второй – по изменению номера столбца. Причем один из этих циклов находится внутри другого. Такие циклы называются вложенными.
Цикл, который стоит внутри другого цикла называется внутренним. А цикл, который содержит внутри себя другой цикл, называется внешним.
Внешний цикл начинает работу раньше, чем внутренний, и включает последний целиком в свою рабочую часть.
6.1. Ввод-вывод двумерных массивов
Пусть требуется осуществить ввод значений двумерного массива Z, состоящего из N строк и M столбцов (размерность NxM).
Решение. Сначала введем размерность массива: Nи M.
Дальнейшие действия зависят от того, как будут вводиться элементы массива: по строкам или по столбцам.
Построчный ввод матрицы более естественен - так нам ее удобнее читать. В этом случае внешним циклом будет цикл по номеру строки i=1,2,…,N, а внутренним - по номеру столбца j=1,1....,M. Такой ввод рассмотрен на схеме (рис.6.1.). В случае ввода матрицы по столбцам, циклы меняются местами.
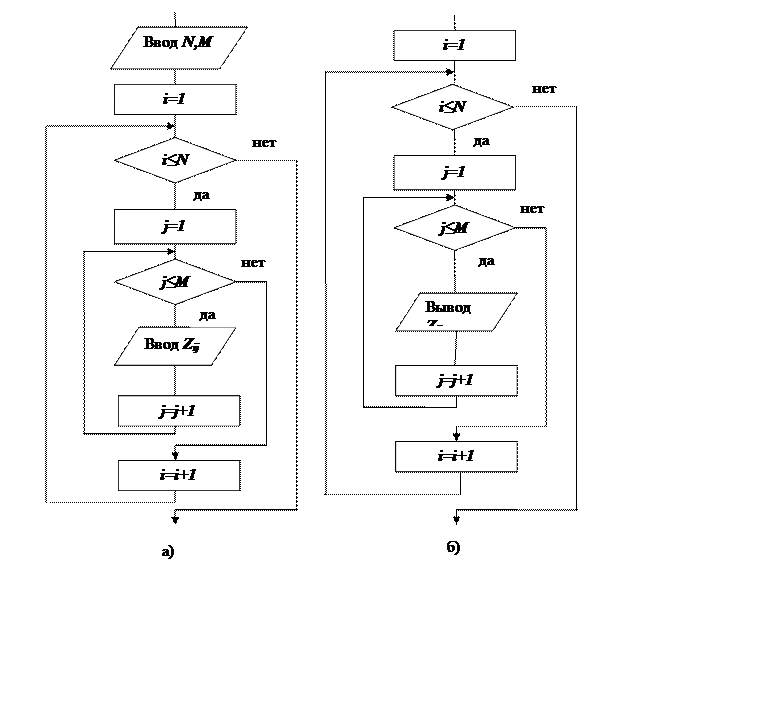
Рис.6.1. Схема алгоритма ввода а) и вывода б) двумерного массива
В
последующих примерах, чтобы сократить запись алгоритма будем использовать для
ввода и вывода матриц обозначения следующего вида: 
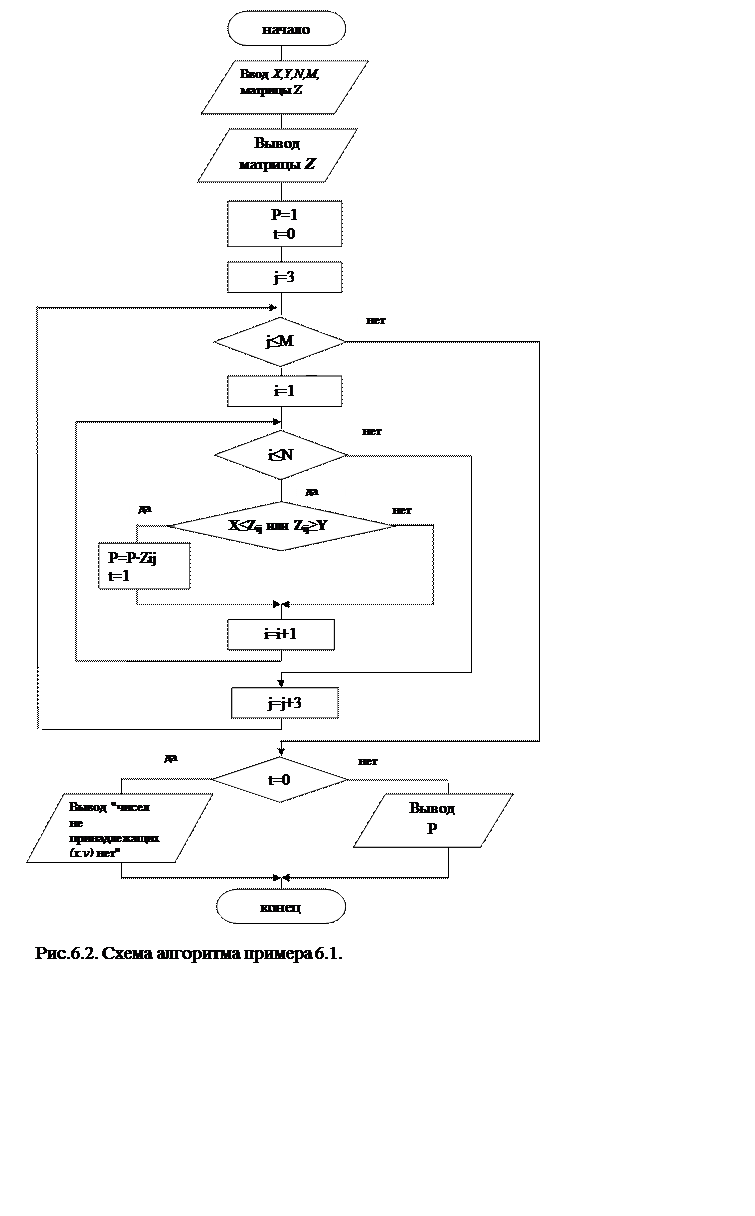
Пример 6.1. Вычислить произведение элементов матрицы, не принадлежащих интервалу (X,Y) и расположенных в столбцах с номерами кратными 3.
Решение. Обозначим номер строки через i, а номер столбца – j . Поскольку в вычислении произведения участвуют элементы (причем только не принадлежащие (X,Y)) столбцов 3,6,…,M, оформим вложенные циклы следующим образом:
- внешний – по номеру столбца: j=3,6,…,M;
- внутренний – по номеру строки: i=1,2,3,…,N.
Величина t позволяет судить о том, были в матрице элементы принадлежащие (X,Y) (когда t=1) или нет (когда t=0).
Схема алгоритма приведена на рис. 6.2.
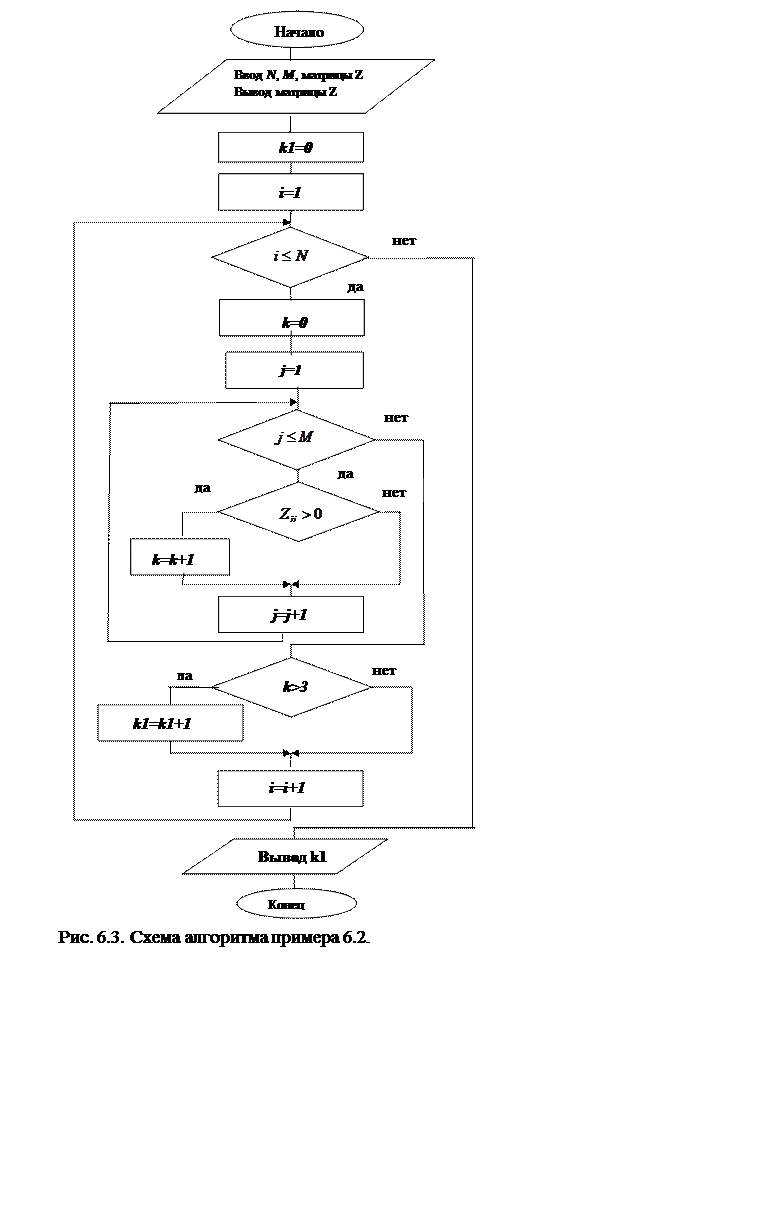
Пример 6.2. Определить количество строк матрицы, в которых содержатся более трех положительных элементов.
Решение. Для подсчета количества введем две величины:
- k– количество положительных элементов в рассматриваемой строке (каждый раз при переходе на новую строку k=0);
- k1 – количество строк, содержащих более трех элементов.
Вложенные циклы оформим здесь следующим образом:
- внешний – по номеру строки: i=1,2,3,...,N;
- внутренний – по номеру столбца: j=1,2,...,M.
Схема программы представлена на рис.6.3.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.