Для нашей задачи:
- стакан с водой – это x(n_min);
- стакан с молоком – это x(n_sad);
- пустой стакан – дополнительная величина R.
Перелив (перестановку) можно осуществить в три этапа
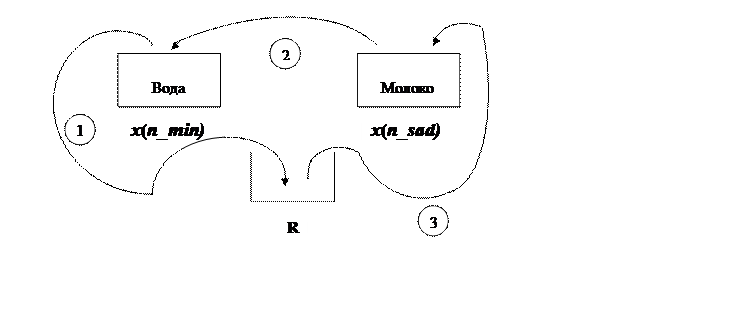
Рис.5.7. Иллюстрация алгоритма перестановки
В принятых нами обозначениях это запишется следующим образом:
![]() R=x(n_min)
R=x(n_min)
x(n_min)=x(n_sad)
x(n_sad)=R
Замечание 1. В следующих случаях перестановка не нужна или невозможна:
а) n_min=n_sad – перестановка не нужна, т.к. элемент, с которым нужно осуществить перестановку и есть минимальный;
б) n_sad= n_min-1 (т.е. перестановка с предыдущим элементом), а n_min=1 - перестановка невозможна, т.к. нет предыдущего элемента;
в) n_sad=n_min+1 (т.е.перестановка см последующим элементом), а n_min=N – перестановка невозможна, т.к. нет последующего элемента.
Поэтому, прежде чем делать перестановку нужно проверить одно из перечисленных условий (какое – зависит от поставленной задачи), чтобы решить вопрос о ее необходимости или возможности.
Замечание 2. В рассмотренном нами алгоритме перестановки роль вспомогательной величины R (третьего стакана) может сыграть величина min.
Тогда перестановка осуществляется в два этапа

Пример 5.3. Найти минимальный элемент и поменять его местами с предыдущим элементом массива.
Решение. Схема алгоритма для решения этой задачи приведена на рис.5.8.
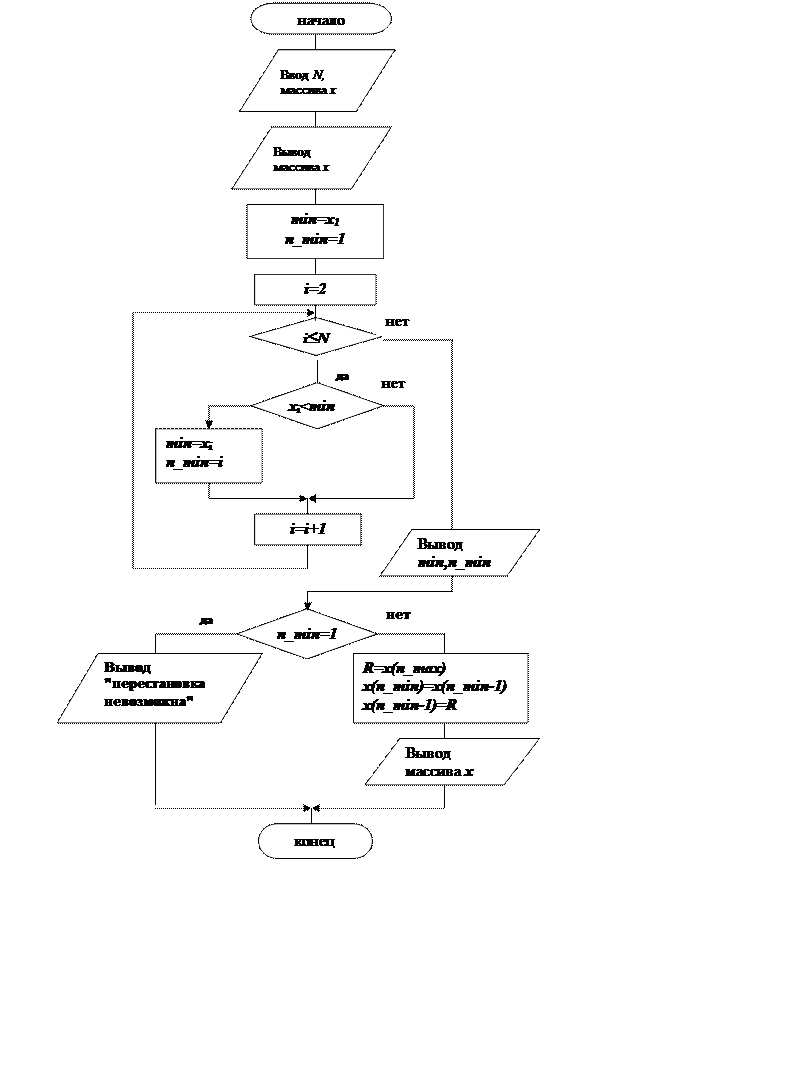
Рис. 5.8. Схема алгоритма примера 5.3
Пусть имеется массив x, состоящий изN элементов. Необходимо сформировать новый массив y, в который войдут те элементы массива x, для которых выполняется некоторое условие, например, только положительные значения.
Решение. Обозначим через i величину, которая будет являться индексом у элементов массива x; она же будет показывать, сколько элементов в нем уже просмотрено. Обозначим через k величину, которая будет являться индексом у элементов массива Y; она же будет показывать, сколько элементов в нем уже сформировано. Тогда для решения задачи применим следующий алгоритм:
1. Зададим значение k=0.
2. Организуем цикл по i=1,2,…,N,
внутри которого будем осуществлять проверку условия попадания xiв новый массив.
В случае выполнения этого условия выполняем следующие действия: k=k+1
yk=xi
Пример 5.4.Даны два числовых массива. Сформировать третий массив из положительных элементов первого массива и отрицательных элементов обоих массивов.
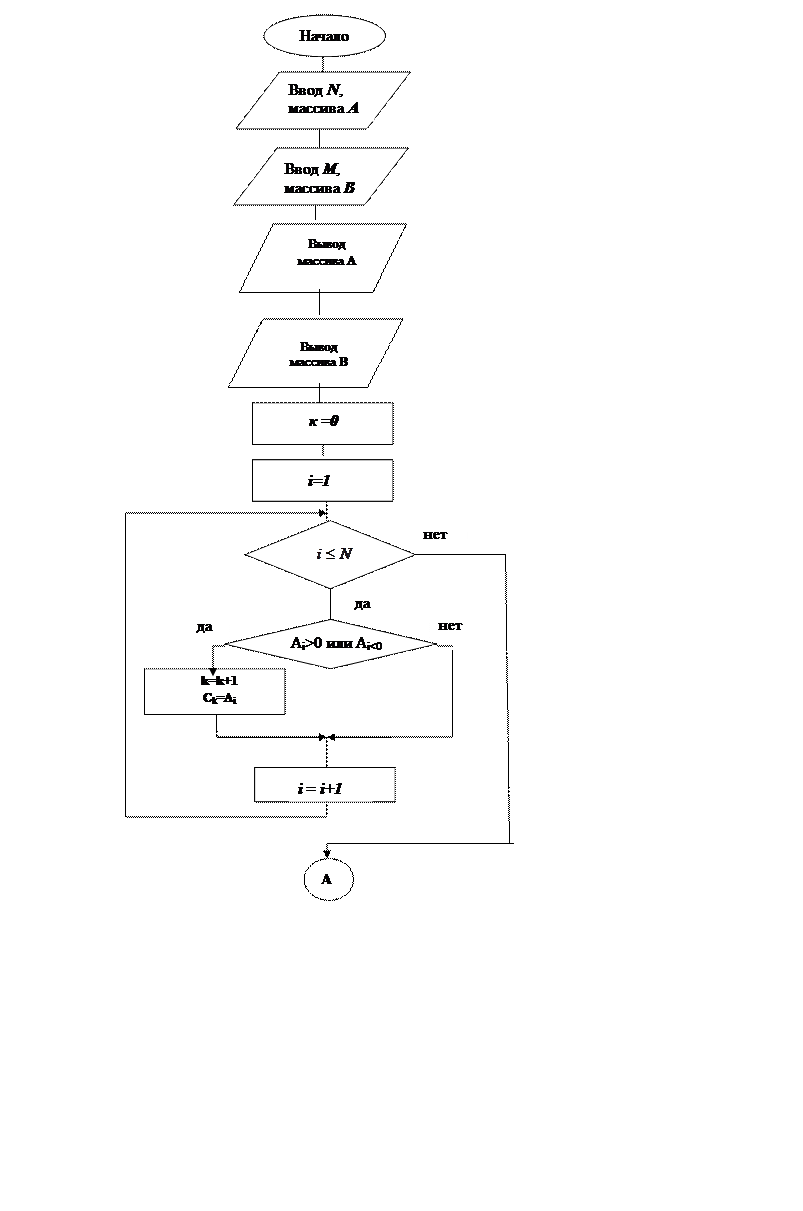
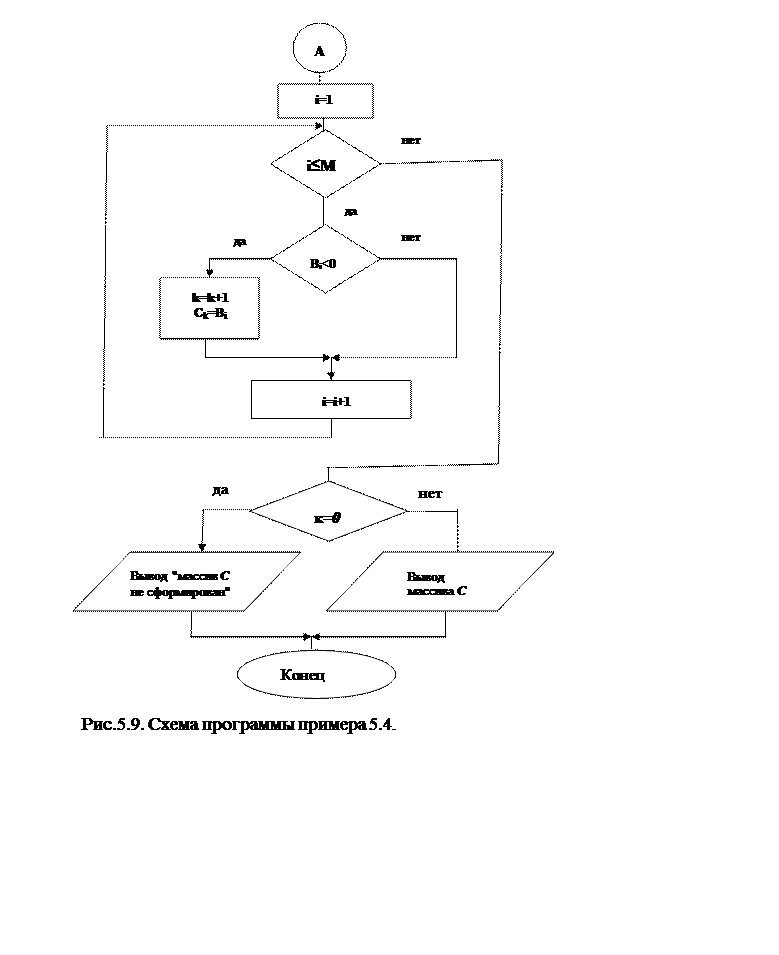
Решение. Обозначим исходные массивы какAиB, состоящие из NиM элементов, соответственно. Вновь формируемый массив обозначим через C. При его формировании описанный выше алгоритм нужно применить дважды: сначала для массива A, а затем для массива B. Но во втором случае установку значения k=0 делать не нужно, т.к. числа из массива В будут дописываться в уже сформированную из элементов массива А часть массива С. Схема алгоритма приводится на рис.5.9.
Массив называется упорядоченным по возрастанию, если для любой соседней пары его элементов выполняется условие
![]()
Массив называется упорядоченным по убыванию, если для любой соседней пары его элементов выполняется условие
![]()
Замечание 1. Термин: упорядоченный по
не убыванию означает выполнение условия ![]() , а
термин: упорядоченный по не возрастанию – условие
, а
термин: упорядоченный по не возрастанию – условие ![]() .
.
Использование при поиске упорядоченных массивов очень часто значительно повышает эффективность поиска (за счет сокращения времени), поскольку в этом случае просматривается не весь массив, а только его часть.
Например, массив содержит упорядоченный по алфавиту (по возрастанию) список фамилий студентов. По условию задачи нужно выдать список фамилий, начинающихся с буквы "А". В этом случае, как только в массиве попадется фамилия, начинающаяся с буквы "Б" поиск можно завершить; а если бы список не был упорядочен, то пришлось бы просматривать весь массив. Упорядочивание массива (или другой термин – сортировка) осуществляется при помощи специальных алгоритмов, которые рассмотрены в [2].
Пример 5.5.В упорядоченном по не убыванию массиве из чисел найти количество отрицательных чисел, и определить, есть ли в массиве нули.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.