Основы алгоритмизации: Практическое пособие к контрольным работам по курсу «Информатика», страница 2

Линии в схемах должны подходить к символу либо слева, либо сверху, а исходить либо справа, либо снизу. Линии должны быть направлены к центру символа. При необходимости линии в схемах нужно разрывать во  избежание излишних пересечений или слишком длинных линий, а также, если схема состоит из нескольких страниц. Соединитель в начале разрыва называется внешним соединителем, а соединитель в конце разрыва – внутренним соединителем. Совместно с символом комментария можно указать, с какой страницы, или на какую страницу схемы совершается переход.

Примеры:

Внешний соединитель                             Внутренний соединитель

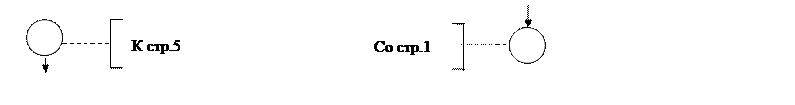
Несколько выходов из символа можно  показывать:

·  несколькими линиями отданного символа к другим символам;

·  одной линией от данного символа, которая затем разветвляется в соответствующее число линий.

Примеры:

          Каждый выход из символа нужно пометить значениями соответствующих условий, чтобы показать логический путь, который он представляет, с тем, чтобы эти условия и соответствующие ссылки были идентифицированы.

Примеры:

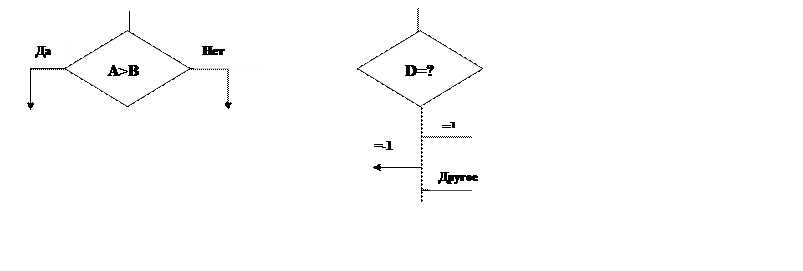
При всем разнообразии структур алгоритмов можно выделить четыре типовых структуры (рис.1.1), из которых как из кирпичиков, можно построить здание алгоритма любой сложности: следование, ветвление, цикл и выбор.

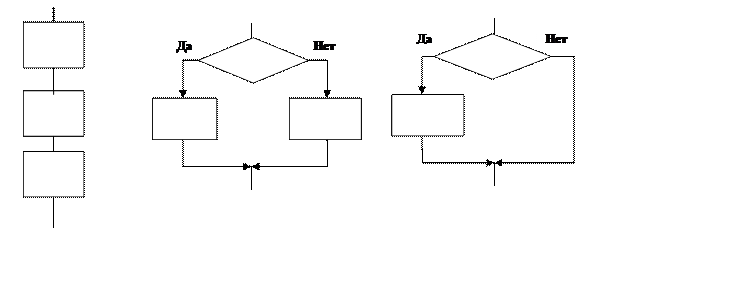
          а)                                      б)                                              в)

Рис. 1.1. Типовые структуры алгоритмов: а) - следование; б, в) – ветвление (полное и неполное).

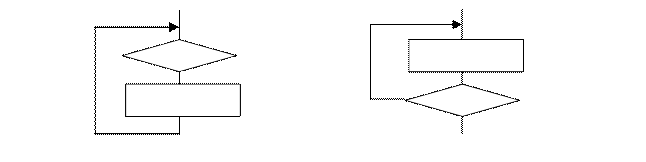
                                       а)                                              б)

Рис.1.2. Типовые структуры алгоритмов: а) – цикл с предусловием; б) – цикл с постусловием.

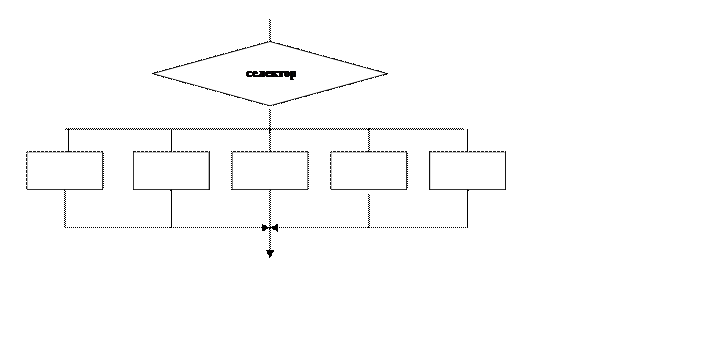
Рис.1.3. Типовая структура выбор.

          Типовые структуры хороши тем, что все они имеют одну точку входа и одну точку выхода. Это упрощает просмотр и понимание алгоритма и сокращает количество возможных ошибок, сделанных при составлении схемы и время на их поиск. Типовые структуры могут быть вложенными друг в друга, например, символ, входящий в структуру следование может включать в себя структуры ветвление или цикл, а каждая из ветвей структур ветвление или выбор может содержать структуры следование, цикл или еще одно ветвление и выбор.

2.  Типы алгоритмов

На основе перечисленных в разделе 1 структур строятся следующие типы алгоритмов:

·  линейный (на основе структуры следование); характеризуется тем, что все действия, определяемые  символами, входящими в схему, выполняются последовательно, в порядке их написания;

·  разветвляющийся (на основе структур ветвление и выбор): характеризуется тем, что в ходе выполнения, решение задачи идет только по одному из имеющихся направлений, выбор которого зависит от выполнения  заданного условия:

·  циклический (на основе структуры цикл): характеризуется многократным повторением определенной группы действий.

В последующих разделах на конкретных примерах рассматриваются все вышеперечисленные типы алгоритмов.

Сразу же оговоримся, что в рассмотренных примерах исходные данные задаются корректно, т.е. например, если в расчете функции (пример 5.1) используется ln(x), то значение x  будет задано большим, чем 0, т.к. в противном случае произойдет ошибка вычисления (логарифм для х≤0 не существует). Поэтому схема алгоритма проверки условия х>0 не предусматривает. Хотя, конечно, в серьезных задачах нужно обязательно проверять все вводимые значения на предмет: допустимы ли они  или нет.

3.  Линейные алгоритмы

Пример 3.1. Вычислить значение функции

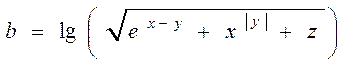  при известных значениях x, yи z.

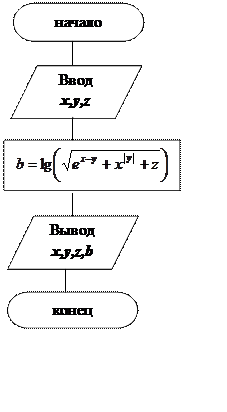Решение. Исходными данными для расчета являются значения x, yи z. Их значения нужно ввести с какого – либо устройства. Значение b становится известными только после расчета по формуле. Тогда, чтобы оно стало известно нам, его нужно вывести на устройство вывода.

     Схема алгоритма представлена на рис. 3.1.

Рис.3.1. Схема алгоритма к примеру 3.1.

Замечание. Алгоритм предусматривает вывод не только полученного результата, но и всех введенных исходных данных. Это следует делать всегда по двум причинам:

§  Появляется возможность контроля правильности ввода данных;

§  Если результат выводится в виде распечатки на принтер,  всегда можно видеть,  при каких исходных данных он получен

Пример 3.2.  Вычислить высоту и площадь равнобедренного треугольника с основанием а и углом при основании a.