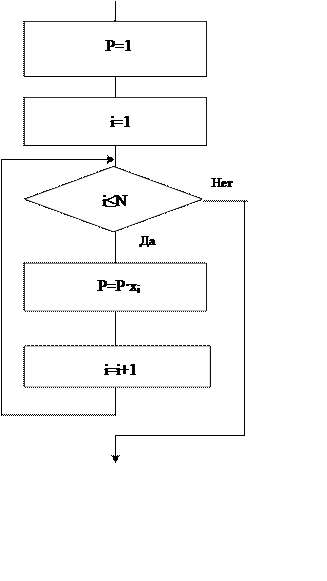
Оформим указанные действия в виде графической схемы (рис.5.5(а))
а) б)
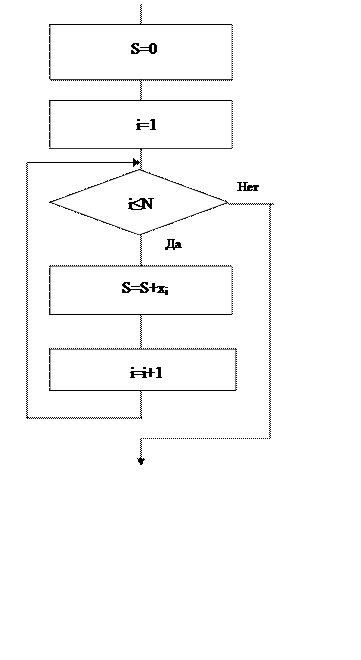
Рис.5.5. Графическая схема алгоритма вычисления суммы (а) и произведения (б)
Замечание1. Вычисление произведения элементов одномерного массива производится по аналогичному алгоритму.
Пусть нужно вычислить
.
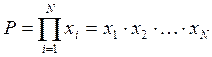Тогда:
1. Зададим P=1.
2. Организуем цикл по i=1,2,...,N на каждом шаге которого будем выполнять следующее действие:
.
Графическая схема такого алгоритма представлена на рис.5.5(б).
Замечание 2. Если нужно суммировать или перемножать не все элементы массива, а только лишь те, для которых выполняется заданное условие, то перед суммированием (умножением) необходимо проверять это условие, и выполнять суммирование (умножение) только тогда, когда условие выполняется. Такой случай рассмотрен в примере 5.2.
Замечение 3. Определение количества элементов массива, значения которых удовлетворяют некоторому условию (например, xi>0) осуществляется по алгоритму, во многом схожему на алгоритм вычисления суммы. Обозначим количество через K.
Тогда:
1. Зададим K=0.
2. Организуем цикл по i=1,2, …, N на каждом шаге которого будем проверять выполнение условия для i-элемента массива. В случае, если условие выполняется производим действие K=K+1.
Пример 5.2. Найти среднее арифметическое положительных чисел среди элементов массива, стоящих на нечетных местах и произведение чисел массива, меньших заданного С.
Решение. Особенностью данной задачи является то, что она состоит из 2-х подзадач, осуществляющих обработку элементов одного и того же массива:
1)
Вычисление среднего
арифметического положительных чисел. Для ее решения понадобиться цикл по i=1,3,5,…,N, т.е. с шагом изменения =2. Среднее арифметическое можно вычислить по
формуле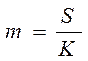 
, где S – сумма
положительных чисел, стоящих на нечетных местах, а K-их количество. Перед его вычислением нужна проверка условия K≠0, т.к.
в противном случае (когда таких чисел нет) расчет m невозможен.
2) Вычисление произведения чисел, меньших заданного С. Для ее решения нужен цикл по i=1,2,…,N. А чтобы убедиться, что числа < C в массиве были, введем в схему дополнительную величину t. Перед началом вычисления произведения установим для нее значение =0, а как только будет найдено значение элемента массива <C, установим t=1. Таким образом, t играет роль сигнала о наличии в массиве чисел <C. Схема алгоритма приведена на рис.5.6.
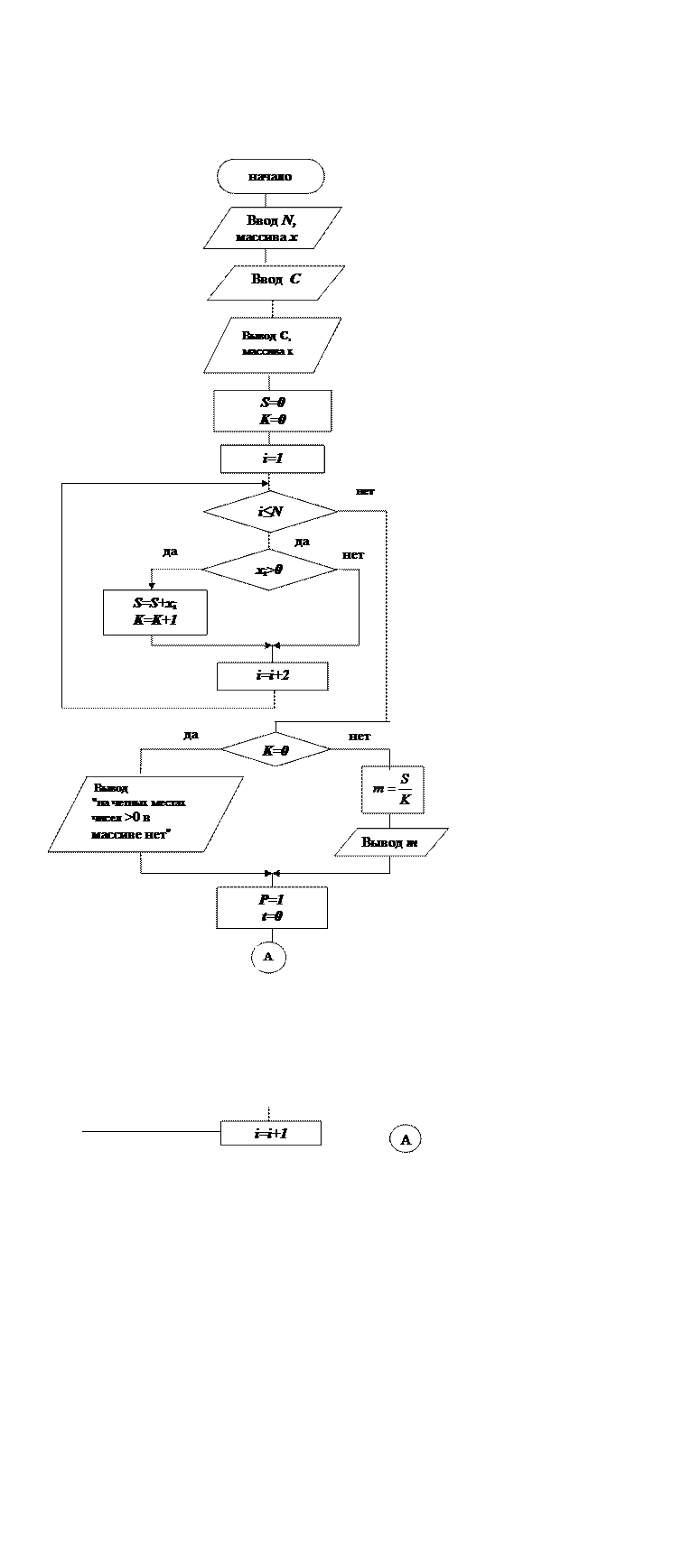
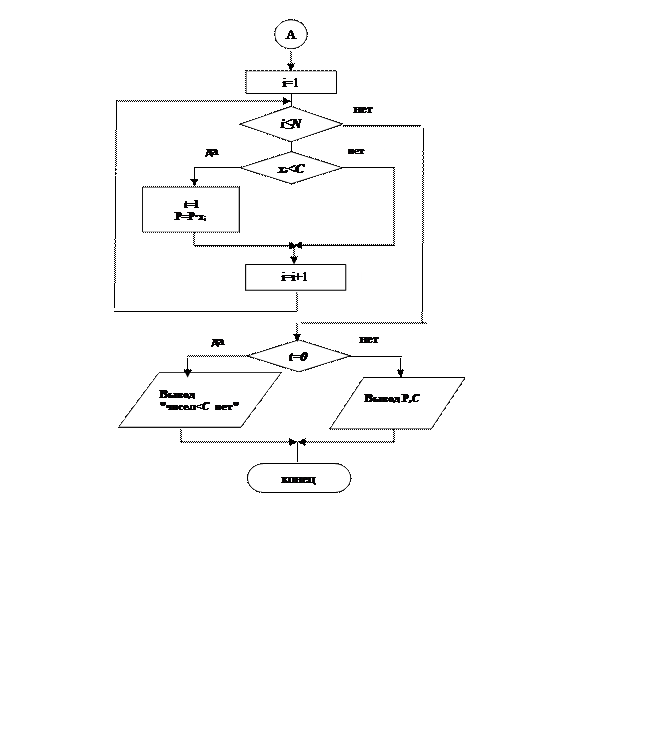
Рис.5.6. Схема алгоритма примера 5.2
Пусть в одномерном массиве x из N числовых элементов нужно найти минимальное (наименьшее) значение и его порядковый номер, например, в следующем массиве
|
х1 |
х2 |
х3 |
х4 |
х5 |
х0 |
|
-3 |
12 |
-5 |
-7 |
20 |
101 |
наименьшее значение =-7, а порядковый номер этого элемента =4.
Обозначим наименьшее значение величиной min, а его порядковый номер величиной n_min. Тогда для их поиска воспользуемся следующим алгоритмом:
1. Зададим min=x1и n_min=1
(тем самым как бы предполагая, что минимальный элемент – это первый).
2. Организуем цикл по i=2,3,…,N внутри которого будем проверять условие xi<min.
В случае выполнения этого условия делаем замену
min=x1
n_min=i
(Таким образом, при выполнении п.2 мы значения всех остальных элементов сравним с min и в случае нахождения меньшего значения, делаем замену).
Замечание. Подобным образом работает и алгоритм нахождения максимального (наибольшего) значения – max и его порядкового номера – n_max. Но в этом случае проверяемое в п.2 условие нужно записать так:
xi>max.
Очень часто возникает задача перестановки найденного минимального x(n_min) или максимального x(n_max) элемента с другим элементом того же массива, номер которого задан x(n_sad).
Описание алгоритма перестановки будем иллюстрировать простым примером: имеются стакан с водой и стакан с молоком; нужно поменять содержимое стаканов (рис.5.7). Ясно, что для этого понадобиться третий, пустой стакан.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.