Итерационные алгоритмы порогового декодирования, страница 3

Используя сведения о значениях весов проверок (предсказание ошибок по спектру весов проверок), можно модифицировать рассмотренные выше алго­ритмы и построить непрерывно-блочный декодер. Этот декодер работает как непрерывный декодер без итераций при отсутствии ошибок, когда Д, )$ Л7.(для этого достаточно одного анализатора ошибок), и как блочный декодер с итерациями, когда вес В_i,₁<=J/2 (также достаточно одного анализатора).

В непрерывно - блочном декодере практически отсутствует "граничный эффект", так как проверка с весом В_i,₁<=J/2, обусловленная ошибками в после­дующем блоке, не может оказаться в блоке декодирования без ошибок. Переключение режимов работы анализатора оши­бок в зависимости от значения В_i,₁ производится блоком управления декодера.

Предсказание ошибок по значениям весов проверок (предсказание качест­ва канала) позволяет синтезировать алгоритм адаптивного итерационного деко­дирования и построить адаптивный блочный декодер или адаптивный непре­рывно - блочный декодер, в которых число итераций контролируется по значе­ниям весов проверок.

Число итераций (или число ступеней декоди­рования) может достигать 5-6 в зависимости от значений вероятности ошибки в канале р. В то же время в большинстве случаев декодирование успешно происходит на первой, второй итерациях (когда в блоке ошибок нет или их ма­ло). Если декодирование производится программно на микро-ЭВМ универ­сального назначения, имеется необходимость освободить процессор возможно раньше для выполнения других операций. Поэтому целесообразно организо­вать декодирование с учётом качества канала. Необходимость дополнительных итераций контролируется по значениям весов в блоке декодирования.

Если в множестве весов проверок отсутствуют значения В_i,₁<=J/2, итера­ции декодируемого блока прекращаются и декодер переключается в режим де­кодирования следующего блока. В таком декодере число итераций является случайным и зависит от вероятности ошибок в канале связи, в результате скорость декодирования в среднем увеличивается .

Среднее число итераций может быть определено как математическое ожидание случайной величины

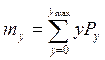
где y_тах - максимально возможное число итераций (обычно ограничивается 5-6

итерациями); Ру - распределение числа итераций, которое определяется свой-

ствами канала связи и структурой декодера.

В канале с независимыми ошибками у=1, когда в декоррелируемом блоке

нет ошибок. Следовательно,

Р1=(1-р)п,

,

,

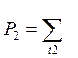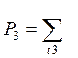где t2,t3 - конфигурации ошибок, исправляемые на второй и третьей итера-

циях и так далее.

В реальных каналах в большинстве случаев у=1 или 2. На рисунке 5.16 приведено распределение Py для канала с независимыми ошибками, при декодировании сверточного кода (406,203) с постоянными и неременными уровнями порога на итерациях. Видно, что изменение уровней порога на итерациях практически не меняет распределение числа итераций в области малых значений р , в то же время с увеличением р заметно увеличивается среднее число итераций в декодере с переменным порогом, что еще раз подтверждает положительный эффект от изменения уровня порога, заключающийся в том, что при большим числе ошибок процесс их исправления распределяется но итерациям более равномерно в сравнении с декодированием при постоянном уровне порога на итерациях.

На рисунке 5.18 приведена структурная схема блочного порогового деко­дера сверточных кодов R=. Декодер работает аналогично показанному на рисунке 5.12 за исключением тою, что в ОЗУ-1 принятый блок разделяется на n0 последовательностей, одна из которых Р(х) является проверочной, а k0= п0 -1 последовательностей I1(x) . . . 1k0(х) являются информационными и за­писываются в отдельные блоки памяти: озу1 -2... ОЗУко-2.