Переходные процессы в электроэнергетических системах: Методические указания к выполнению лабораторных работ, страница 8

1.  Выполнить анализ статической устойчивости простейшей электроэнергетической системе (ЭЭС) в нормальном и послеаварийном режимах.

2.  Исследовать электромеханический переходный процесс в простейшей ЭЭС при коротком замыкании на линии:

- исследовать влияние места КЗ на динамическую устойчивость ЭЭС;

- исследовать влияние вида КЗ на динамическую устойчивость ЭЭС.

3.  Выработать умения оценивать динамическую устойчивость графическим методом, приобрести навыки расчета показателей динамической устойчивости ЭЭС, совершенствовать умения практического приложения теоретических знаний к анализу результатов экспериментальных исследований.

4.  Совершенствовать навыки работы с ПЭВМ при выполнении прикладных инженерных задач. 

3.2. Краткие сведения из теории

Динамическая устойчивость – это способность системы возвращаться в исходный (или близкий к нему) режим после большого возмущения.

Для исследования динамической устойчивости системы используют динамические характеристики – это связи параметров, полученные при условии, что они зависят от времени.

Если статическая устойчивость характеризует установившийся режим системы, то при анализе динамической устойчивости выявляется способность системы сохранять синхронный режим работы при больших его возмущениях. Большие возмущения возникают при различных видах коротких замыканий, отключении линий электропередачи, генераторов, трансформаторов и пр. К большим возмущениям относятся также изменения мощности крупной нагрузки, потеря возбуждения какого-либо генератора, включение мощных двигателей. Одним из следствий возникшего возмущения является отклонение скоростей вращения роторов генераторов от синхронной (качания роторов генераторов системы).

Если после какого-либо возмущения взаимные углы роторов примут определенные значения (их колебания затухнут около каких-либо новых значений), то считается, что динамическая устойчивость сохраняется. Если хотя бы у одного генератора ротор начинает проворачиваться относительно поля статора, то это признак нарушения динамической устойчивости. В общем случае о динамической устойчивости системы можно судить по зависимостям d = f(t), полученным в результате совместного решения уравнений движения роторов генераторов. Но существует более простой и наглядный метод, основанный на энергетическом подходе к анализу динамической устойчивости, который называется графическим методом или методом площадей.

Рассмотрим простейшую систему, когда электростанция G работает через двухцепную линию на шины бесконечной мощности (рисунок 3.1,а). Условие постоянства напряжения на шинах системы (U = const) исключает качания генераторов приемной системы и значительно упрощает анализ динамической устойчивости. Схема замещения системы показана на рисунке 3.1,б. Генератор входит в схему замещения переходным сопротивлением  и переходной ЭДС (генератор с АРВ пропорционального типа). Мощность, выдаваемая генератором в систему, равна мощности турбины и обозначена Р_о, угол ротора генератора относительно поля статора – d_о. Характеристика мощности, соответствующая нормальному (доаварийному) режиму, может быть получена из известного выражения без учета второй гармоники, что вполне допустимо в практических расчетах [1]. Принимая  = Е',получим выражение характеристики мощности в следующем виде:

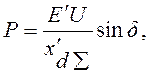                                                 (3.1)

где

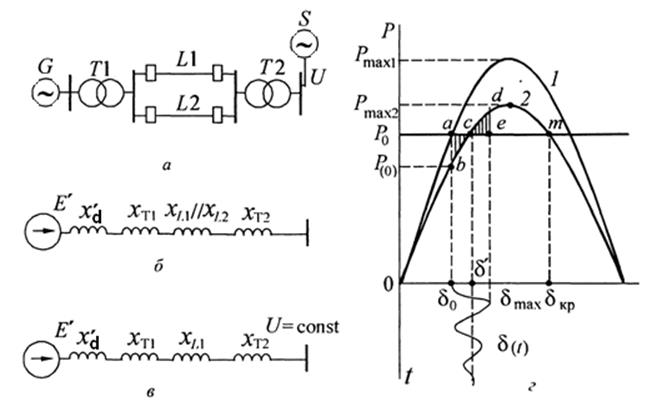
Рисунок 3.1 – К анализу динамической устойчивости простейшей системы: а – принципиальная схема; б – схема замещения в нормальном режиме; в – схема замещения в послеаварийном режиме; г – графическая иллюстрация динамического перехода: характеристики нормального и послеаварийного режимов (кривые 1, 2 соответственно)

Зависимость Р = f(d)  для нормального режима приведена на рисунке 3.1,г (кривая 1).

Предположим, что линия L2 внезапно отключается. Рассмотрим работу генератора после ее отключения. Схема замещения системы после отключения линии показана на рисунке 3.1,в. Суммарное сопротивление послеаварийного режима