Переходные процессы в электроэнергетических системах: Методические указания к выполнению лабораторных работ, страница 2

2. Лабораторная работа 1. Исследование электромагнитного переходного процесса в электрической системе

2.1. Цели лабораторной работы

1.  Исследовать электромагнитный переходный процесс в простейшей трехфазной электрической цепи:

- исследовать влияния удаленности точки короткого замыкания (КЗ) на полный ток короткого замыкания и его составляющие;

- исследовать влияние фазы включения КЗ на полный ток короткого замыкания и его составляющие.

2.  Приобрести навыки расчета токов КЗ в трехфазных цепях, выработать умения оценивать параметры тока трехфазного КЗ по осциллограммам переходного процесса, совершенствовать умения практического приложения теоретических знаний к анализу результатов экспериментальных исследований.

3.  Совершенствовать навыки работы с ПЭВМ при выполнении прикладных инженерных задач.

2.2. Краткие сведения из теории

Электромагнитный переходный процесс рассматривается при условии, что внезапное КЗ произошло в простейшей электрической цепи (рисунок 2.1), присоединенной к источнику неограниченной мощности, т.е. к источнику, действующее значение напряжения на зажимах которого можно практически считать неизменным при любых токах в цепи.

а)
б)
Рисунок 2.1 – Принципиальная схема простейшей системы (а) и схема ее замещения (б)

В силу симметрии исходной трехфазной схемы как до, так и после КЗ, в дальнейшем рассмотрим физические процессы в одной из фаз.

Ток, предшествующий КЗ (фаза А), определяется выражением:

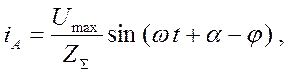
где U_max – амплитуда напряжения на входе трехфазной схемы;

Z_Σ – суммарное сопротивление схемы в нормальном режиме;

j – аргумент суммарного сопротивления Z_Σ (определяет сдвиг фаз между напряжением и током);

a – угол между горизонталью и вектором U_А, называется фазой включения КЗ (см. рисунок 2.2).

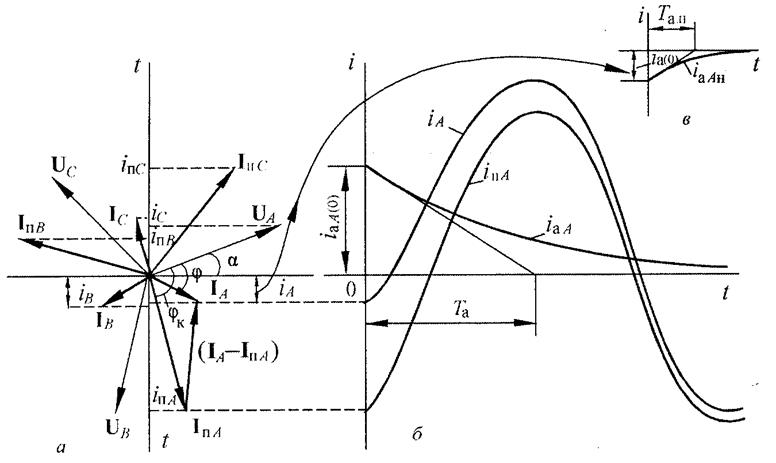
Рисунок 2.2 – Векторная диаграмма (а) и изменение токов в левой и правой частях схемы простейшей системы (б), (в)

После включения выключателя Q, который создает КЗ, схема делится на две части. Ток в правой части существует до тех пор, пока энергия, запасенная в индуктивности нагрузки L_н, не перейдет в тепло в активном сопротивлении нагрузки r_н.

Для этой части схемы дифференциальное уравнение (из теоретических основ электротехники):

или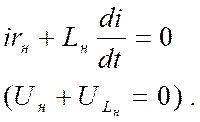          

Решение данного уравнения относительно тока имеет  вид:

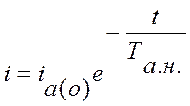 – свободный ток,

где 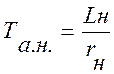 – постоянная времени цепи нагрузки;

i_а(0) – начальное значение свободного (апериодического) тока.

В левой части схемы, кроме свободного тока,  под действием приложенного синусоидального напряжения с неизменной амплитудой U_mах  должен установиться вынужденный периодический ток с амплитудой больше предшествующего (до КЗ) из-за снижения суммарного сопротивления цепи.

Дифференциальное уравнение для левой части (фаза А) по закону Кирхгофа примет вид:

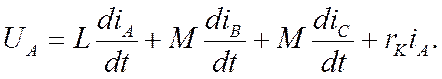
Учитывая, что в симметричном режиме           ,

можно записать иначе:

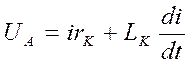,                                          (2.1)

где L_K– результирующая индуктивность фазы: L_K = L – M;

М – взаимная индуктивность фаз.

Решение дифференциального уравнения (2.1), т.е. мгновенное значение полного тока КЗ, имеет вид:

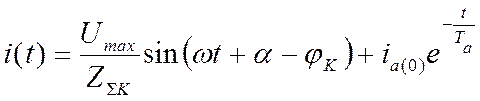,                    (2.2)

где  – полное сопротивление короткозамкнутого участка цели; j_К – аргумент Z_K (сдвиг фаз между Uи I в зависимости от характера сопротивления); Т_а - постоянная времени цепи КЗ; i_a(0) – апериодическая составляющая тока при начальных нулевых условиях.

Первое слагаемое в (2.2) – периодическая (вынужденная) составляющая тока КЗ. Второе слагаемое – апериодическая (свободная) составляющая.

Начальное значение свободной составляющей i_а(0) определяется из начальных условий КЗ (т.е. при t = 0). Ток предшествующего режимаi₀ равен сумме начальных значений периодической и апериодической составляющих тока КЗ (в силу неразрывности тока в цепи с индуктивностью), т.е.

i_o = i_n(o) + i_a(o),

тогда

i_a(o) = i_o - i_n(o) =[I_max sin (wt + a - j) - I_{n max} sin (wt+a - j_k)]/_{при t=0} =

= I_max sin (a - j)- I_{n max} sin (a - j_k),

гдеI_max– амплитуда тока до КЗ;

      I_nmax – амплитуда периодической составляющей тока КЗ.