Вычисляем
поперечные силы ![]() .
.
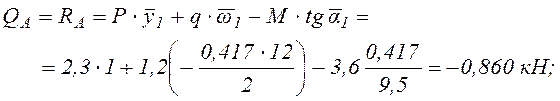
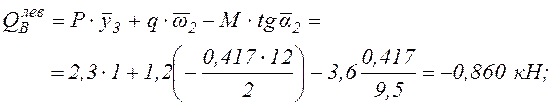
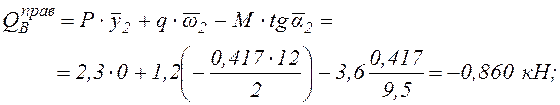
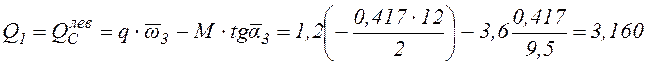 кН;
кН;
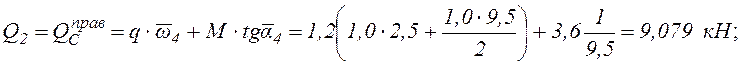
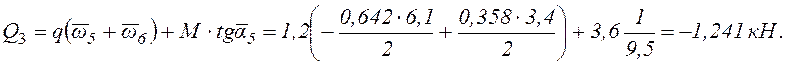
Вычисляем изгибающие моменты МА, МС, М3 .
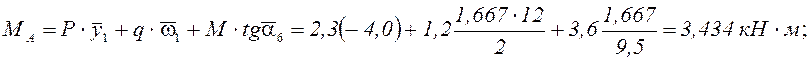
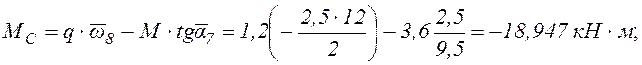
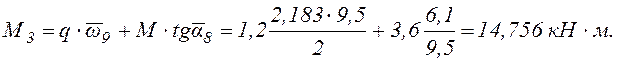
Такие же значения с точностью до третьего знака после запятой получены ранее при построении эпюр Q, M.
3. ПРИМЕР РАСЧЁТА СТАТИЧЕСКИ ОПРЕДЕЛИМОЙ
ПЛОСКОЙ РАМЫ
Для рамы (рис. 13) построить и проверить эпюры продольных N, поперечных Qсил и изгибающих моментов M.

Рис. 13. Расчётная схема рамы
Решение выполняем в такой последовательности.
1) Определяем реакции опор, задав предполагаемые
направления реакций и обозначив их ![]() .
.
Для рамы в целом можем составить только три независимых уравнения равновесия:
![]() ;
; ![]() ;
;
![]() ;
;
![]() . (3.1)
. (3.1)
![]() ;
; ![]() ;
;
![]() ;
;
![]() . (3.2)
. (3.2)
![]() ;
; ![]() ;
;
![]() ;
;![]() (3.3)
(3.3)
Из условия равновесия правой части рамы ![]() получим дополнительное уравнение и из него
найдём
получим дополнительное уравнение и из него
найдём ![]() .
.
![]() ;
; ![]() ;
; ![]() ;
;
![]() ;
; 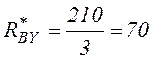 кН.
кН.
Из уравнения (3.1) найдём ![]() .
.
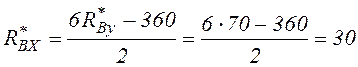 кН.
кН.
Из уравнения (3.3) найдём ![]() .
.
![]() кН.
кН.
Подставив ![]() в уравнение (3.2),
получим
в уравнение (3.2),
получим
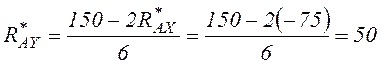 кН.
кН.
Для проверки найденных реакций составим уравнение равновесия рамы в целом, в которое войдут все реакции.
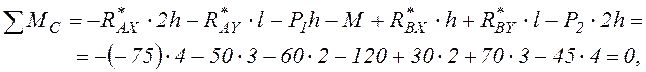
т.е. реакции найдены правильно.
Все реакции, кроме ![]() получены
положительными, т.е. их истинные направления соответствуют предполагаемым.
Истинное направление реакции
получены
положительными, т.е. их истинные направления соответствуют предполагаемым.
Истинное направление реакции ![]() кН – вправо
(предполагаемое направление
кН – вправо
(предполагаемое направление ![]() на расчётной схеме рамы
перечёркнуто и показано истинное).
на расчётной схеме рамы
перечёркнуто и показано истинное).
В дальнейшем будем использовать в расчётах истинные
направления реакций ![]() .
.
Для упрощения построения эпюр на участках ![]() и
и ![]() найдём
реакции в шарнире С (рис. 13).
найдём
реакции в шарнире С (рис. 13).

Рис. 14. Рама, разъединённая (расчленённая) по шарниру С
Для левой части рамы (рис. 14,а), имеем:
![]() ;
; ![]() ;
; ![]() кН;
кН;
![]() ;
; ![]() ;
;
![]() кН.
кН.
Аналогично для правой части (рис. 14,б)
![]() ;
; ![]() ;
; ![]() кН;
кН;
![]() ;
; ![]() ;
; ![]() кН.
кН.
Дополнительным подтверждением правильности определения
реакций служит соблюдение условий ![]() ,
, ![]() , как внутренних усилий в шарнире
, как внутренних усилий в шарнире ![]() .
.
2) Строим эпюры ![]() (рис.
15), выражая законы их изменения на отдельных участках (см. рис. 14).
(рис.
15), выражая законы их изменения на отдельных участках (см. рис. 14).
Участок
![]() ;
; ![]() м).
м).
![]() кН;
кН; ![]()
![]() ;
;
![]() ; а)
; а) ![]() ;
; ![]() ;
;
![]() б)
б)
![]() м;
м; ![]()
![]() .
.
Участок ![]() ;
; ![]() .
.
![]() кН
кН ![]() ;
;
![]()
![]()
![]() ;
;
![]() ; а)
; а) ![]() м;
м; ![]()
![]() ;
;
б) ![]() м;
м; ![]() кН·м;
кН·м;
Участок ![]() ;
; ![]() .
.
![]() кН
кН ![]() ;
;
![]() ;
; 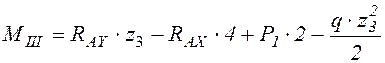 ;
;
а) ![]() ;
; ![]() кН;
кН; ![]() кН·м;
кН·м;
б) ![]() м;
м; ![]() кН;
кН; ![]() кН·м
кН·м
в) 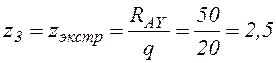 м;
м; ![]() кН·м;
кН·м;
Участок ![]() ;
; ![]() .
.
![]()
![]() ;
;
![]() ;
; 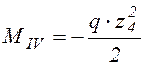 ;
;
а) ![]() ;
; ![]() ;
; ![]() ;
;
б) ![]() м;
м; ![]() кН;
кН; ![]() кН·м;
кН·м;
Участок ![]() ;
; ![]() .
.
![]() кН
кН ![]() ;
; ![]() кН
кН
![]() ;
;
![]() ; а)
; а) ![]() ;
; ![]() ;
;
б) ![]() м;
м; ![]() кН·м.
кН·м.
Участок ![]() ;
; ![]() .
.
![]() кН
кН ![]() ;
; ![]() кН
кН
![]() ;
;
![]() ; а)
; а) ![]() ;
; ![]() кН·м;
кН·м;
б) ![]() м;
м; ![]() кН·м.
кН·м.
Участок ![]() ;
; ![]() .
.
![]()
![]() ;
;
![]() кН
кН ![]() ;
;
![]() ; а)
; а) ![]() ;
; ![]() ;
;
б) ![]() м;
м; ![]() кН·м.
кН·м.

Рис. 15. Эпюры внутренних усилий в раме
Примечание.
При определении знака изгибающего момента и при изображении эпюр ![]() и
и![]() на
вертикальных участках (стойках) расчётную схему рассматриваем, располагаясь
справа от неё, как это принято в техническом черчении.
на
вертикальных участках (стойках) расчётную схему рассматриваем, располагаясь
справа от неё, как это принято в техническом черчении.
Построенные по участкам эпюры ![]() и
и
![]() проверим одним из способов, выделяя
отдельные узлы рамы и загружая их всеми (внешними и внутренними) усилиями (рис.
16).
проверим одним из способов, выделяя
отдельные узлы рамы и загружая их всеми (внешними и внутренними) усилиями (рис.
16).

Рис. 16. Проверка равновесия узлов рамы
Направления
и значения внутренних усилий в узлах взяты с эпюр ![]() и
и ![]() (см. рис. 15) с учётом принятых правил
знаков.
(см. рис. 15) с учётом принятых правил
знаков.
Из рис. 16 видно, что для каждого из узлов
удовлетворяются три условия равновесия ![]() ,
, ![]() и
и ![]() . Это
подтверждает правильность построения эпюр.
. Это
подтверждает правильность построения эпюр.
Предлагается самостоятельно убедиться в том, что на всех участках рамы удовлетворяются и дифференциально-интегральные зависимости (1.1), (1.2).
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Дарков, А.В. Строительная механика: учебник для вузов / А.В. Дарков,
Н.Н. Шапошников. – 9-е изд., испр. – СПб. Лань, 2004. – 655 с.
2. Руководство к практическим занятиям по курсу строительной механики: Статика стержневых систем. Учеб. пособие для строит спец. вузов / Под общ. ред. Г.К. Клейна. – 4-е изд., перераб. и доп. – М.: Высш. школа, 1980, – 384 с.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.