Известно, что определённый интеграл численно равен
площади ![]() графика подынтегральной функции в пределах
графика подынтегральной функции в пределах
![]() , т.е. в нашем случае
, т.е. в нашем случае ![]() и
и ![]() могут
быть вычислены через площади эпюр
могут
быть вычислены через площади эпюр ![]() и
и ![]()
![]() Эпюру q не строят, но
она повторяет схему внешней распредёленной нагрузки. Следует лишь помнить, что
положительная qнаправлена
вверх.
Эпюру q не строят, но
она повторяет схему внешней распредёленной нагрузки. Следует лишь помнить, что
положительная qнаправлена
вверх.
Таким образом, выражения (1.3) можно представить в виде
Q(ξ)![]() M(ξ)
M(ξ)![]() . (1.4)
. (1.4)
и использовать их как для контроля, так и для построения эпюр Q и M.
Расчёт стержневых систем на постоянную и особенно на временную и подвижную нагрузки (последние два вида расчётов в данной работе не рассматриваются) эффективно выполняется с использованием линий влияния. Это – новоедля студентов важное в курсе «Строительная механика» понятие, и его изучению следует уделить особое внимание.
Линия влияния – это график, изображающий закон
изменения какого-либо фактора (реакции, внутреннего усилия, перемещения) в
фиксированном сечении, возникающего от действия «подвижной» безразмерной единичной
силы ![]() , занимающей различные положения на
сооружении. Значение исследуемого фактора на этом графике откладывается под соответствующим
положением единичной силы.
, занимающей различные положения на
сооружении. Значение исследуемого фактора на этом графике откладывается под соответствующим
положением единичной силы.
Линии влияния реакций и внутренних усилий, которые определены заданием, могут быть построены с использованием статического (аналитического) или кинематического методов. Отметим, что при расчёте балок наиболее эффективным является кинематический метод, однако суть теории линий влияния может быть уяснена, если надёжно усвоена идея статического метода.
Вычисление исследуемых факторов (реакций, внутренних усилий), возникающих от заданной нагрузки, с использованием соответствующих линий влияния производится путём так называемого «загружения» линий влияния по правилам, в основе которых заложен принцип независимости действия сил.
2. ПРИМЕР РАСЧЁТА СТАТИЧЕСКИ ОПРЕДЕЛИМОЙ
МНОГОПРОЛЁТНОЙ БАЛКИ
Для
балки (рис.1,а) построить эпюры поперечных сил Q и
изгибающих моментов M, линии влияния реакций ![]() , поперечных
сил
, поперечных
сил ![]()
![]() ,
,![]() и изгибающих моментов
и изгибающих моментов ![]() (сечения 1 и 2 взяты
бесконечно близко к опоре С слева и справа от неё). Используя линии влияния,
вычислить указанные реакции и внутренние усилия.
(сечения 1 и 2 взяты
бесконечно близко к опоре С слева и справа от неё). Используя линии влияния,
вычислить указанные реакции и внутренние усилия.

Рис. 1. Расчётная и поэтажная схемы балки
Решение задачи производим в следующей последовательности.
1. Изображаем поэтажную схему балки (рис. 1,б), выделяя основную балку АВ, вспомогательную балку ВСD второго этажа и вспомогательную DEF третьего этажа. Чтобы случайно не учесть дважды силу Р, приложенную к шарниру, рекомендуется на поэтажной схеме приложить её к нижележащей балке, т.е в данном случае – к основной балке.
2. Определяем реакции опор и строим эпюры Q и M в отдельных балках.
В первую очередь рассмотрим самую верхнюю вспомогательную балку DEF (рис. 2,а).
Опорные реакции рассмотрим из условий равновесия:
![]()
![]() ;
; ![]()
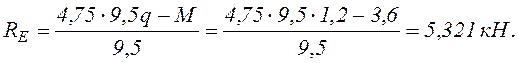
![]()
![]()
![]()
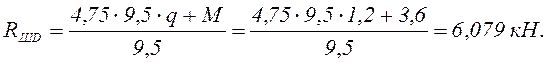
Проверка:
![]()
т.е. реакции ![]() ,
, ![]() найдены правильно.
найдены правильно.
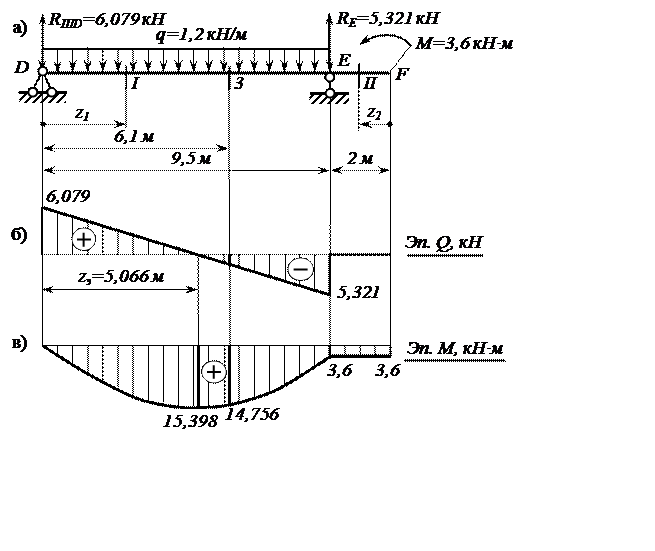
Рис. 2. Расчётная схема и эпюры Q, M балки DEF
Эпюры Q и M (рис.2,б,в) строим по участкам.
Участок DE; (![]() ).
).
![]() ;
; 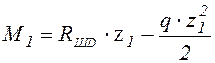 .
.
а) ![]() ;
; ![]() кН;
кН; ![]() ;
;
б) ![]() м;
м; ![]() кН;
кН; ![]() кН·м;
кН·м;
в) 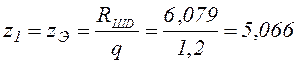 м;
м; ![]() кН·м;
кН·м;
г)![]() м;
м; ![]() кН;
кН; ![]() кН·м.
кН·м.
Участок EF; ![]() м).
м).
![]() ;
; ![]() кН
м
кН
м ![]() .
.
Далее рассмотрим вспомогательную балку BCD,
расположенную этажом ниже. Кроме заданной нагрузки эта балка «нагружена» также
реакцией ![]() найденной для вышерасположенной балки DEF,
но направленной в противоположную сторону, т.е. вниз (рис. 3,а).
найденной для вышерасположенной балки DEF,
но направленной в противоположную сторону, т.е. вниз (рис. 3,а).
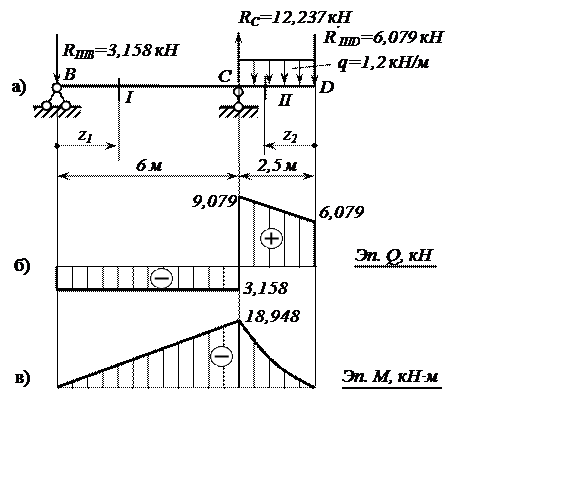
Рис.3. Расчётная схема и эпюры Q, M балки BCD
Определяем опорные реакции:
![]()
![]()
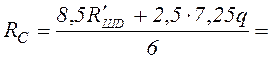
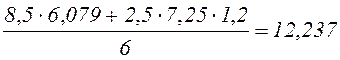 кН.
кН.
![]() ;
; ![]()
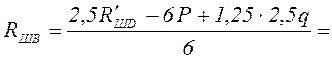
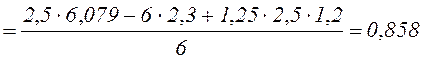 кН.
кН.
Проверка:
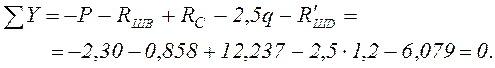
Строим эпюры Q, M (рис. 3,б,в).
Участок ВС; ![]() м).
м).
![]() кН
кН ![]() ;
;
![]() ;
;
а) ![]() ;
; ![]() ; б)
; б) ![]() м;
м; ![]() кН·м.
кН·м.
Участок CD; ![]() м).
м).
![]() ;
; 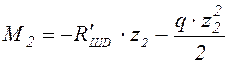 ;
;
а) ![]() ;
; ![]() кН;
кН; ![]() ;
;
б) ![]() м;
м; ![]() кН;
кН; ![]() кН·м.
кН·м.
В последнюю очередь рассмотрим основную балку АВ (рис. 4,а).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.