Расчет статически определимых многопролётных балок и плоских рам: Методические указания к выполнению контрольной и расчётно-проектировочной работы по дисциплине "Строительная механика", страница 4

Так, например, для построения модели линии влияния  устраним опорный стержень C и в направлении положительной  (вверх) сообщим сечению С единичное линейное перемещение (рис. 7).

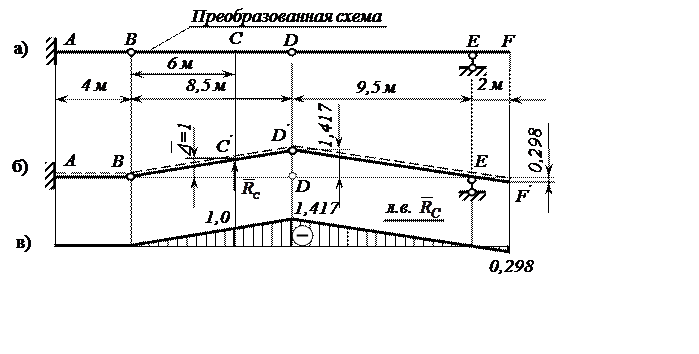
Рис. 7. Построение модели линии влияния  кинематическим методом

В этом случае стержень AB останется неподвижным, так как связан с «землёй» жёстким защемлением. Стержень BCD повернётся при этом относительно шарнира B так, что шарнир D переместится вверх, а стержень DEF повернётся относительно шарнирно-подвижной опоры E. Перемещения сечений C, D, F, которые легко вычислить из геометрических соотношений, и дадут нам значения линий влияния  в характерных точках.

Для построения линий влияния внутренних усилий стержневую систему необходимо преобразовать в механизм, устранив соответствующую внутреннюю связь.

Внутренние связи «обеспечивают» полную неподвижность относительно друг друга двух частей стержня, условно рассечённого в исследуемом сечении. Эти три связи можно представить наложенными следующим образом (рис. 8,а).

Шарнирное соединение стержней представляется наложением двух связей (рис. 8,б).

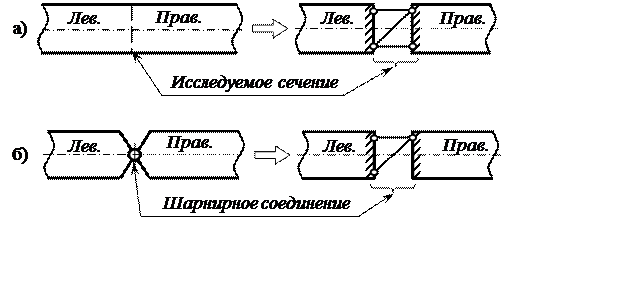
Рис.8. Схема наложения внутренних связей

Устранение одной из горизонтальных связей в сплошном сечении обеспечивает возможность взаимного поворота левой и правой частей стержня на угол , а устранение наклонной связи – взаимного линейного смещения на  без взаимного поворота левой и правой частей (рис. 9,а).

На схеме преобразованной стержневой системы устранение угловой связи представляется врезанием в исследуемое сечение шарнира, а устранение линейной поперечной связи – введением ползуна (рис. 9,б).

Устранение наклонной связи в шарнирном соединении разрешает взаимное вертикальное перемещение на , но не накладывает ограничений на взаимный поворот (рис. 9,в), и на преобразованной стержневой системе представляется «размыканием» (разъединением) шарнира.

Для построения линий влияния изгибающего момента стержневой системе задаётся во врезанном шарнире относительный угол поворота  в направлении положительного  (рис. 10,а), а для линий влияния поперечной силы – относительное поперечное смещение  в направлении положительной .

Рис. 9. Способы устранения связей в исследуемом сечении при

построении линий влияния кинематическим методом

Построение линий влияния изгибающих моментов ,  и поперечных сил  кинематическим методом показано на рис. 10, 11.

Рис. 10. Построение моделей линий влияния изгибающих моментов

Заметим, что, определяя значения перемещений в преобразованной стержневой системе, следует исходить из того, что  и  – бесконечно малые (возможные) перемещения, поэтому горизонтальными перемещениями пренебрегаем, а вертикальные перемещения на моделях линий влияния вычисляем как дуги окружности соответствующих радиусов.

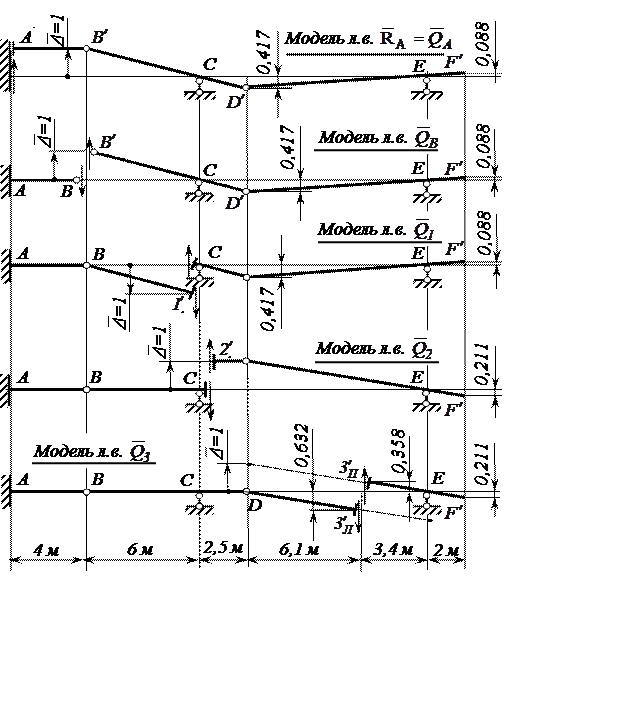
Рис. 11. Построение моделей линий влияния поперечных сил

Следует также обратить внимание на то, что на модели линии влияния поперечных сил оси стержней справа и слева от введённого ползуна остаются параллельными между собой (рис. 11,а,в,г,д). В то же время оси стержней слева и справа в «разомкнутом» шарнире не параллельны (рис. 11,б).

7) Загружаем линии влияния.

Для удобства поместим все построенные выше линии влияния под расчётной схемой балки (рис. 12).

Загружение линии влияния какого-либо усилия  выполняется по формуле

 ,

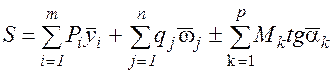где        – значение линии влияния  под сосредоточенной силой ;

Рис. 12. Загружение линий влияния

 – численное значение площади линии влияния  под равномерно распределённой нагрузкой ;

 – численное значение тангенса угла наклона линии влияния  под сосредоточенным моментом ;

 – число сосредоточенных сил, участков распределённых нагрузок, сосредоточенных моментов, соответственно.

Положительные направления нагрузок ,  – вниз.

Произведение  принимается со знаком «+», если направления момента М_kи отсчёта угла противоположны, и со знаком «–», если эти направления совпадают.