![]() м);
м);
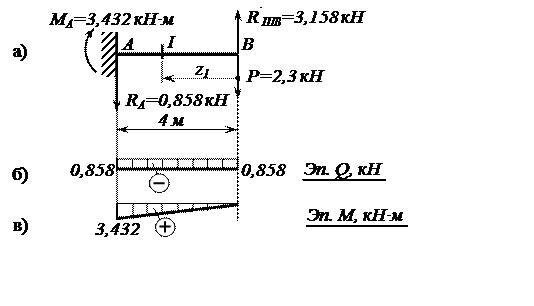
Рис. 4. Расчётная схема и эпюры Q, M балки АВ
![]() кН
кН ![]() ;
;
![]() ;
;
а) ![]() ;
; ![]() ; б)
; б)
![]() м;
м; ![]() кН.
кН.
Заметим, что эпюры Q и M для этой балки можно построить, не определяя реакции в защемлении. Реакции в защемлении, равные значениям поперечной силы и изгибающего момента в сечении А, направлены в соответствии с правилами знаков Q и M.
3) Эпюры Q и Mдля заданной балки получим, изображая эпюры Q и M отдельных её частей на общей базе (рис. 5,б).
4). Проверим эпюру Q, используя интегральное соотношение (1.4) между Q и q.
Участок АВ.
![]() кН;
кН; ![]() ;
;
![]() кН.
кН.
Участок ВС.
![]() кН;
кН; ![]() ;
;
![]() кН.
кН.
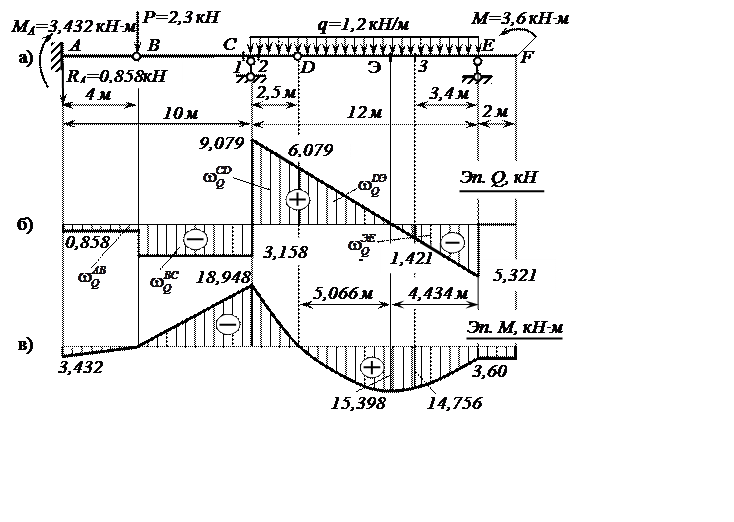
Рис. 5. Расчётная схема и эпюры Q и M заданной балки
Участок СD.
![]() кН;
кН;
![]() кН.
кН.
![]() кН.
кН.
Участок DE.
![]() кН;
кН; ![]() кН;
кН;
![]() кН.
кН.
Участок EF.
![]() ;
; ![]() ;
;
![]() .
.
Заметим, что, определяя ![]() для
каждого последующего участка, выполняем «скачёк» на значение и в направлении
сил, приложенных на границах смежных участков.
для
каждого последующего участка, выполняем «скачёк» на значение и в направлении
сил, приложенных на границах смежных участков.
5). Аналогично предыдущему, выполним проверку эпюры M по эпюре Q, используя интегральное соотношение (1.4) между М и Q.
Участок АВ.
![]() кН м;
кН м; ![]() кН м;
кН м;
![]()
Участок ВС.
![]()
![]() кН м.
кН м.
Участок CD.
![]() кН м;
кН м;
![]() =
=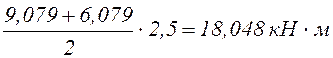 ;
;
![]()
Участок DE.
![]() ;
;
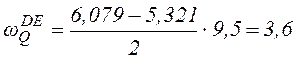 кН
м;
кН
м;
![]() кН м;
кН м;
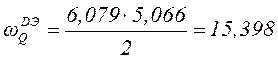 кН м;
кН м;
![]() кН м.
кН м.
Участок ЕF.
![]() кН·м;
кН·м; ![]() ;
; ![]() кН·м.
кН·м.
Нулевые значения изгибающих моментов в шарнирах В
и D и значение изгибающего момента на правом конце балки,
равное сосредоточенному внешнему моменту ![]() кН·м,
соответствуют расчётной схеме.
кН·м,
соответствуют расчётной схеме.
Обратим внимание, что ![]() вычислена
здесь как площадь «перекрученной» трапеции по формуле площади обычной трапеции
с той лишь разницей, что учтены знаки сторон. Эта площадь может быть
представлена и как сумма площадей треугольников, т.е.
вычислена
здесь как площадь «перекрученной» трапеции по формуле площади обычной трапеции
с той лишь разницей, что учтены знаки сторон. Эта площадь может быть
представлена и как сумма площадей треугольников, т.е.
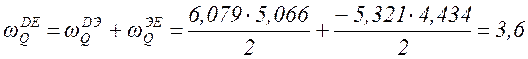
![]() .
.
6) Строим лини влияния, используя статический и кинематический методы.
Для построения некоторых линий влияния, например, ![]() , воспользуемся статическим методом.
, воспользуемся статическим методом.
Аналитические выражения ![]() получим
при различных положениях единичной силы
получим
при различных положениях единичной силы ![]() на
поэтажной схеме балки.
на
поэтажной схеме балки.
а) Пусть ![]() находится в пределах
основной балки
находится в пределах
основной балки ![]() (рис. 6,а), т.е.
(рис. 6,а), т.е. ![]()
![]() . В этом случае
вспомогательные балки
. В этом случае
вспомогательные балки ![]() и
и ![]() без «нагрузки»,
поэтому усилия в шарнирах
без «нагрузки»,
поэтому усилия в шарнирах ![]() .
.
Исследуемые усилия при этом будут:
![]() ;
; ![]() ;
; ![]() ,
,
т.е.
линии влияния ![]() и
и ![]() на
участке
на
участке ![]() нулевые, а линия влияния
нулевые, а линия влияния ![]() - прямая, которую
построим по двум значениям:
- прямая, которую
построим по двум значениям:
а) ![]() ;
; ![]() ; б)
; б) ![]() м;
м;
![]()
![]() .
.

Рис. 6. Построение линий влияния статическим методом
б)
Поместим ![]() на балку ВD(рис. 6,б),
т.е.
на балку ВD(рис. 6,б),
т.е. ![]()
![]() . При этом
. При этом ![]() , т.к. вспомогательная балка DF
без «нагрузки». Реакцию
, т.к. вспомогательная балка DF
без «нагрузки». Реакцию ![]() и усилие в шарнире
и усилие в шарнире ![]() , необходимые для выражения
, необходимые для выражения ![]() , найдём из условия равновесия
вспомогательной балки
, найдём из условия равновесия
вспомогательной балки ![]() .
.
![]()
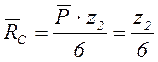 ;
;
![]()
![]()
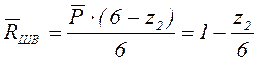 .
.
Момент в защемлении ![]() найдём
из условия равновесия балки AB,
найдём
из условия равновесия балки AB,
![]()
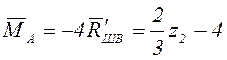 .
.
Внутренние усилия ![]() и
и ![]() зависят от положения
зависят от положения ![]() относительно сечения I:
относительно сечения I:
а) ![]() слева от сечения I,
т.е.
слева от сечения I,
т.е. ![]() м;
м;
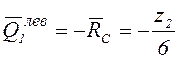 ;
; ![]() ;
;
б) ![]() справа от сечения I,
т.е.
справа от сечения I,
т.е. ![]() ;
;
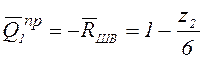 ;
; 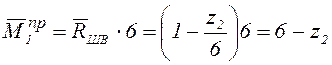 ;
;
(или ![]() ).
).
Вычислим значения ![]() ,
, ![]() и
и ![]() при
характерных положениях
при
характерных положениях ![]() .
.
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
По этим значениям строим линии влияния ![]() ,
, ![]() и
и ![]() на участке BCD.
на участке BCD.
в) ![]() находится на
вспомогательной балке DEF (рис. 6, в), т.е.
находится на
вспомогательной балке DEF (рис. 6, в), т.е. ![]() .
.
В этом случае из условия равновесия вспомогательной
балки DEF найдём 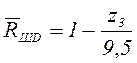 .
.
Зная ![]() , найдём реакцию
, найдём реакцию ![]() и усилие в шарнире
и усилие в шарнире ![]() из
условий равновесия вспомогательной балки BCD.
из
условий равновесия вспомогательной балки BCD.
![]() ;
; ![]() ;
; 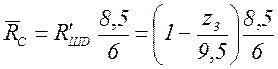 ;
;
![]() ;
; ![]() ;
; 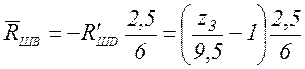 .
.
Выражение ![]() получим из условия
равновесия балки AB.
получим из условия
равновесия балки AB.
![]() ;
; ![]() ;
; 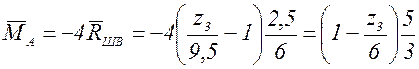 .
.
Внутренние усилия ![]() и
и ![]() выразим через
выразим через ![]() .
.
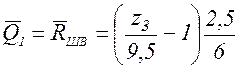 ;
; 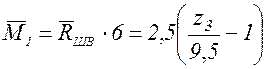 .
.
Вычислим значения линий влияния при характерных
положениях ![]() .
.
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
;
![]()
![]() ;
; ![]() ;
; ![]() .
.
Построенные
таким образом линии влияния ![]() ,
, ![]() и
и ![]() представлены
на рис. 6,г,д,е.
представлены
на рис. 6,г,д,е.
Рассмотрим построение некоторых линий влияния кинематическим методом.
В [1] показано, что если в статически определимой
системе удалить какую-либо связь, превратив тем самым неизменяемую систему в
механизм с одной степенью свободы, и сообщать положительное единичное перемещение
в направлении устраненной связи, то эпюра перемещений точек грузовой линии в
направлении ![]() (для балок – схема перемещений механизма)
будет моделью (копией) линии влияния усилия, соответствующего устранённой связи.
(для балок – схема перемещений механизма)
будет моделью (копией) линии влияния усилия, соответствующего устранённой связи.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.