Расчет статически непределимых плоских рам методом перемещений: Методические указания к выполнению контрольной и расчётно-проектировочной работы по дисциплине "Строительная механика"

Министерство образования и науки Российской Федерации

Федеральное агентство по образованию

Государственное образовательное учреждение высшего

профессионального образования

«Комсомольский-на-Амуре государственный технический университет»

Кафедра «Механика и анализ конструкций и процессов»

РАСЧЁТ СТАТИЧЕСКИ НЕПРЕДЕЛИМЫХ ПЛОСКИХ РАМ

МЕТОДОМ ПЕРЕМЕЩЕНИЙ

Методические указания к выполнению контрольной и расчётно-проектировочной работы по строительной механике

Комсомольск-на-Амуре 2009

УДК 624.04

Расчёт статически неопределимых плоских рам методом перемещений: Методические указания по курсу «Строительная механика» / Сост. В.С. Симонов, Г.С. Лейзерович – Комсомольск-на-Амуре: ГОУВПО «Комсомольский-на-Амуре государственный технический университет», 2009.

 – 17 с.

Методические указания содержат рекомендации по реализации метода перемещений для раскрытия статической неопределимости плоских рам.

Приведен пример расчёта трижды кинематически неопределимой (дважды статически неопределимой) плоской рамы. Решение примера сопровождается необходимыми рисунками и комментариями.

Методические указания предназначены для студентов заочной и дневной форм обучения, изучающих курс «Строительная механика».

Печатается по постановлению редакционно-издательского совета ГОУВПО «Комсомольский-на-Амуре государственный технический университет».

Согласовано с отделом стандартизации.

Рецензент Ю.Н. Чудинов

ВВЕДЕНИЕ

Метод перемещений, как и метод сил, является универсальным (классическим) методом расчёта статически неопределимых стержневых систем. Следует, однако, заметить, что раскрытие статической неопределимости производится через раскрытие кинематической неопределимости, т.е. в качестве неизвестных принимаются не усилия, как в методе сил, а перемещения некоторых (характерных) узлов стержневой системы.

Так же, как и в методе сил, вводятся понятия основной (ОС) и эквивалентной (ЭС ) систем, но принцип их образования из заданной системы (ЗС) принципиально другой. Условия эквивалентности также имеют другой физический (механический) смысл. Теоретические основы метода перемещений рассмотрены в [  ].

Особенности метода перемещений и его применение к расчёту плоских статически неопределимых рам покажем ниже на конкретном примере. В качестве примера рассмотрим ту же раму, что и в методических указаниях «Расчёт плоских статически неопределимых рам методом сил».

1. РАСЧЁТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМОЙ ПЛОСКОЙ РАМЫ МЕТОДОМ ПЕРЕМЕЩЕНИЙ

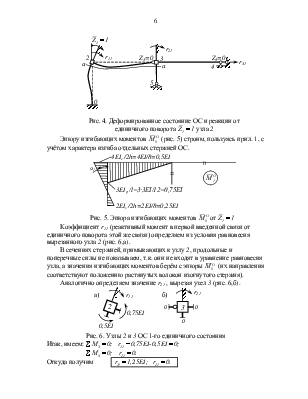
Раскрыть статическую (кинематическую) неопределимость (рис. 1) и построить эпюру изгибающих моментов

Рис.1 Расчётная схема рамы

Решение выполняем в такой последовательности.

1) Определяем число неизвестных метода перемещений.

Общее число неизвестных находим как сумму неизвестных угловых перемещений n_у,равных общему числу жёстких узлов, и независимых линейных перемещений n_лвсех узлов, равных степени свободы преобразованной шарнирной схемы рамы.

Заданна рама имеет два жёстких узла – 3 и 5, т.е. n_у=2.

Шарнирную схему рамы получим из заданной введением шарниров во все жёсткие узлы и заменой жёстко защемлённой опоры шарнирно неподвижной (рис.2).

Рис.2. Преобразованная шарнирная схема рамы

Степень свободы шарнирной схемы рамы вычислим по формуле

.

Число дисков равно числу стержней, т.е. D=4. Приведенное число шарниров (простых шарниров) Ш=3 (один в узле 3 и два – в узле 5). Число опорных связей С_О=5. Тогда

n_л=w=3·4 -2·3 -5=1.

Этим неизвестным перемещением является горизонтальное перемещение, одинаковое для  узлов 3,5,6.

Таким образом, общее число неизвестных (степень кинематической неопределимости)

.

2) Образуем основную систему (ОС), введя в жёсткие узлы «плавающие» заделки (угловые связи), а в узел 6 – линейную горизонтальную связь, запрещающие возможные перемещения узлов рамы. Отметим, что «плавающая» заделка отличается от обычной жёсткой тем, что она препятствует только лишь повороту узла и не лишает его линейной подвижности.

3) Загрузив ОС заданной нагрузкой и указав предполагаемые направления неизвестных перемещений Z₁, Z₂, Z₃, получим эквивалентную систему (ЭС) метода перемещений (рис. 3). Заметим, что это условно эквивалентная система, т.к. она изображена в недеформированном виде.

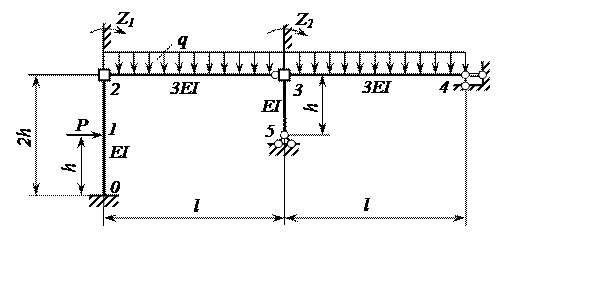
Рис.3. Эквивалентная система

4) Записываем систему канонических уравнений метода перемещений, выражающих условия отсутствия реакций в дополнительно наложенных связях – условия эквивалентности ЗС и ЭС.

r₁₁Z₁+r₁₂Z₂+r₁₃Z₃+R_1P=0;

r₂₁Z₁+r₂₂Z₂+r₂₃Z₃+R_2P=0;

r₃₁Z₁+r₃₂Z₂+r₃₃Z₃+R_3P=0.

Здесь: r_ij (i=1,2,3; j=1,2,3) – реактивное усилие в i-ой дополнительно введенной связи, вызванное единичным перемещением   j-ой дополнительно введенной связи; R_iP – реактивное усилие в i-ой связи, вызванное заданной внешней нагрузкой.

Реакции r_ij, R_iРимеют положительный знак в том случае, когда их направления совпадают с принятым направлением Z_i.

Реакции r_ij= r_jiв силу теоремы о взаимности реакций (аналогично теореме о взаимности перемещений δ_ij= δ_ji – см. метод сил).