Расчет статически непределимых плоских рам методом перемещений: Методические указания к выполнению контрольной и расчётно-проектировочной работы по дисциплине "Строительная механика", страница 2

5) Используем статический метод для вычисления реакций (коэффициентов) r_ijи R_iР(свободных членов) системы канонических уравнений.

Для вычисления r_ijи R_iРстроим (точнее – изображаем) так называемые единичные и грузовую эпюры изгибающих моментов в ОС. Поскольку ОС метода перемещений представляет собой совокупность независимых статически неопределимых балок при двух способах наложения опорных связей, построение названных эпюр сводится к «копированию» решений для наиболее часто встречающихся случаев, приведенных в прил. 1.

Чтобы найти реакции r₁₁, r₂₁ и r₃₁задаём первой введенной связи единичный поворот  при Z₂=Z₃=0 и изображаем схему деформации ОС (рис. 4).

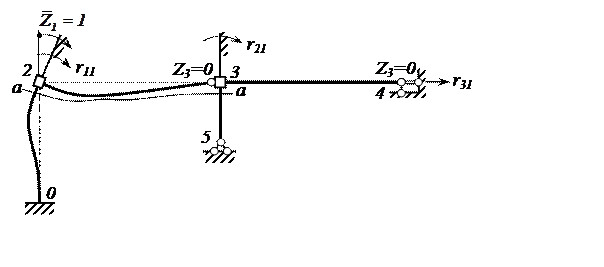
Рис. 4. Деформированное состояние ОС и реакции от

единичного поворота  узла 2

Эпюру изгибающих моментов  (рис. 5) строим, пользуясь прил. 1, с учётом характера изгиба отдельных стержней ОС.

Рис. 5. Эпюра изгибающих моментов от

Коэффициент r₁₁(реактивный момент в первой введенной связи от единичного поворота этой же связи) определяем из условия равновесия вырезанного узла 2 (рис. 6,а).

В сечениях стержней, примыкающих к узлу 2, продольные и поперечные силы не показываем, т.к. они не входят в уравнение равновесия узла, а значения изгибающих моментов берём с эпюры  (их направления соответствуют положению растянутых волокон изогнутого стержня).

Аналогично определяем значение r₂₁ , вырезая узел 3 (рис. 6,б).

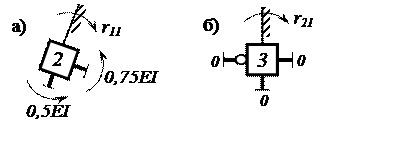
Рис. 6. Узлы 2 и 3 ОС 1-го единичного состояния

Итак, имеем:

                   

Откуда получим           

Значение r₃₁получим из условия равновесия отсечённой сечением

«а – а» части ОС (рис. 7). Изгибающие моменты и реакции в ведённых угловых связях не показываем, т.к. они не входят в уравнение равновесия отсечённой части

Рис. 7. Отсечённая часть ОС 1-го единичного состояния

В сечении стойки 2-1 прикладываем поперечную силу. Её значение равно тангенсу угла наклона эпюры к базовой линии, а направление соответствует направлению отсчёта угла α, т.е. в нашем случае поперечная сила «стремится» повернуть узел 2 против хода часовой стрелки.. Можно воспользоваться и прил. 1, определяя поперечную силу как реакцию в повёрнутом защемлении, но в этом случае возможна ошибка в определении её направления.

Из уравнения равновесия  получим

.

Чтобы найти коэффициенты (реакции) r₁₂, r₂₂ и r₃₂ ,задаём второй введенной угловой связи единичный поворот  при Z₁=Z₃=0 (рис. 8) и, пользуясь прил. 1, строим эпюру изгибающих моментов  (рис. 9).

Рис.8. Деформированное состояние ОС и реакции от

единичного поворота  узла 3

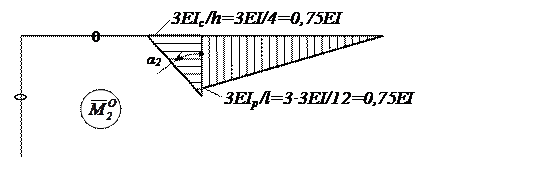
Рис. 9. Эпюра изгибающих моментов  от

Значения r₁₂, r₂₂ определяем из условий равновесия узла 2 (рис. 10,а) и узла 3 (рис. 10,б).

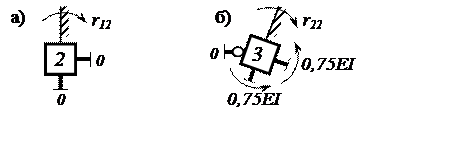
Рис. 10. Узлы 2 и 3 ОС 2-го единичного состояния

Из уравнений равновесия узлов 2 и 3

получим                 r₁₂=0;                   r₂₂=1,5EI.

Для определения r₃₂отделим сечением «б–б» часть ОС (рис. 11).

Рис. 11. Отсечённая часть ОС 2-го единичного состояния

Из условия равновесия отсечённой части ОС

 

получим                           r₃₂=-0,1875EI.

Значения r₁₃, r₂₃иr₃₃ определяем, рассматривая 3-е единичное состояние ОС (рис. 12) – от горизонтального смещения опоры 4 и узлов 2 и 3, соответственно, на . Единичная эпюра изгибающих моментов , построенная с помощью прил.1, приведена на рис. 13.

Рис. 12. Деформированное состояние ОС и реакции от

единичного линейного смещения узлов 2, 3, 4

Рис. 13. Эпюра изгибающих моментов  от

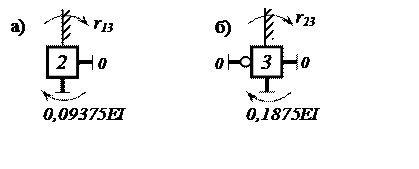
Рис. 14. Узлы 2 и 3 ОС 3-го единичного состояния

Из условий равновесия узла 3 (рис. 14.а) и узла 5 (рис. 14,б) находим:

 

Убеждаемся, что

Значение r₃₃получим из условия равновесия отсечённой сечением

«в–в» части ОС (рис. 15).

Рис. 15. Отсечённая часть ОС 3-го единичного состояния

Для вычисления свободных членов системы канонических уравнений R_iPстроим с помощью прил.1 и ,учитывая деформированное состояние ОС (рис. 16), грузовую эпюру изгибающих моментов  (рис. 17).

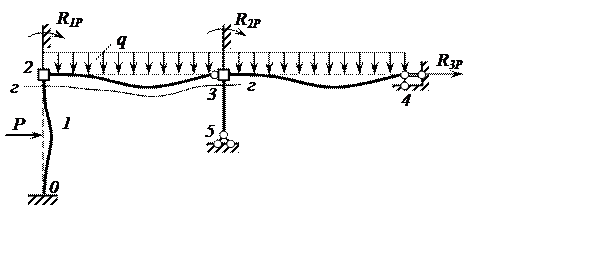
Рис. 16. Деформированное состояние ОС и реакции от нагрузки

Рис. 17. Грузовая эпюра изгибающих моментов в ОС

Рассматривая равновесие узла 2 (рис. 18,а) и узла 3 (рис. 18,б), определяем R_1P и R_2P:

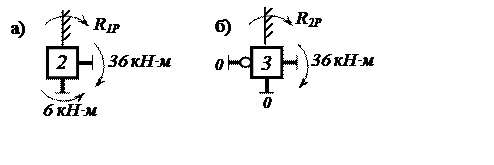
Рис. 18. Узлы 2 и 3 ОС грузового состояния

 

Из уравнения равновесия части ОС, отсечённой сечением «г–г»

(рис. 19), находим R_3P.

Рис. 19. Осечённая часть ОС грузового состояния

Выполним проверку вычислений r_ijи R_iP. Такая проверка необязательна, но желательна, чтобы в случае неправильных вычислений зря не тратить время на продолжение решения.

Проверку вычисления r_ij осуществляем перемножением суммарной единичной эпюры изгибающих моментов  (рис.19), построенной суммированием единичных эпюр (), самой на себя.

Рис. 19. Суммарная единичная эпюра изгибающих моментов

Перемножение выполним по готовым формулам

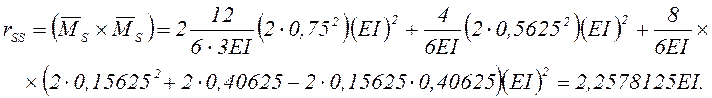
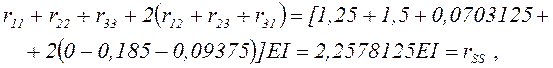
что подтверждает правильность вычислений r_ij. Может быть допущено незначительное расхождение результатов, обусловленное вычислительными погрешностями.