Расчет статически непределимых плоских рам методом перемещений: Методические указания к выполнению контрольной и расчётно-проектировочной работы по дисциплине "Строительная механика", страница 3

Для проверки вычислений R_iP строим эпюру изгибающих моментов от внешней нагрузки  (рис. 20) в любой ОС метода сил, например, рассмотренной в методических указаниях «Расчёт статически неопределимых плоских рам методом сил».

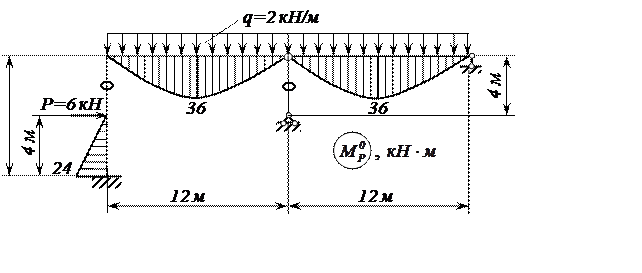
Рис. 20. Эпюра изгибающих моментов от внешней нагрузки

в ОС метода сил

Должно выполняться условие R_1P+R_2P+R_3P=-30-36-3=-69=R_SP, где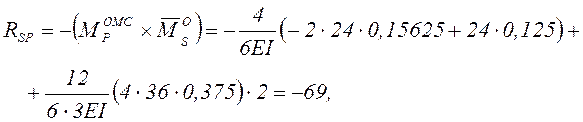

т.е. вычисления выполнены правильно.

Подставим значения r_ijи R_iPв систему канонических уравнений. Разделив всё на EI, получим:

1,25·Z₁         +0·Z₂         -0,09375·Z₃ -30/EI =0;

0·Z₁      +1,5·Z₂          -0,185·Z₃ -36/EI =0;

-0,09375·Z₁ -0,1875·Z₂ +0,0703125·Z₃+3/EI =0.

Решаем систему канонических уравнений, определяя тем самым неизвестные угловые Z₁, Z₂ и линейное Z₃ перемещения узлов заданной рамы.

Если нет возможности решить систему уравнений на ЭВМ, то для ручного расчёта можно воспользоваться, например, правилом Крамера (с использованием микрокалькулятора).

Вычисляем определители:

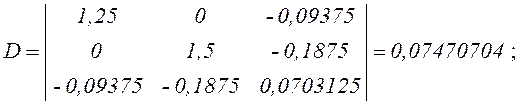
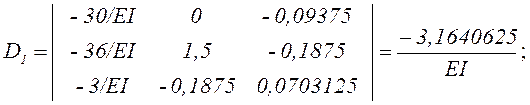
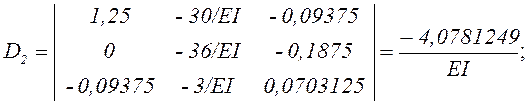
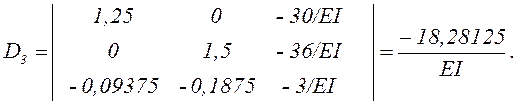
Схема вычисления определителя третьего порядка приведена в прил. 2.

Вычисляем значения Z₁, Z₂ и Z₃

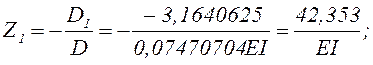
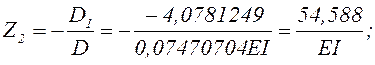
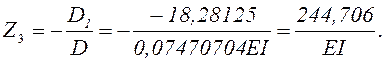
При ручном расчёте рекомендуется выполнить проверку решения, подставляя полученные значения Z₁, Z₂ и Z₃в каждое из уравнений системы.

7) Строим окончательную эпюру изгибающих моментов М_Р .

Как и в методе сил, окончательную эпюру М_Р (рис. 24) получим, суммируя «исправленные» эпюры (рис. 21), (рис. 22), (рис. 23) с эпюрой  (см.  рис. 17). «Исправление» единичных эпюр заключается в умножении всех их значений на соответствующие значения Z_i с учётом знака.

Рис. 21. Исправленная эпюра изгибающих моментов

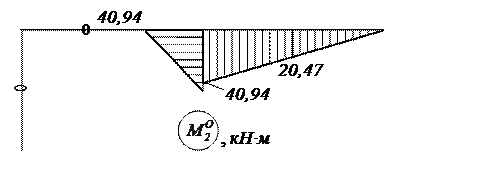
Рис. 22. Исправленная эпюра изгибающих моментов

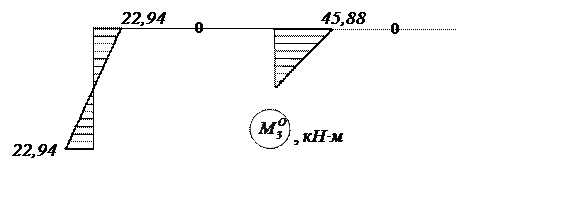
Рис. 23. Исправленная эпюра изгибающих моментов

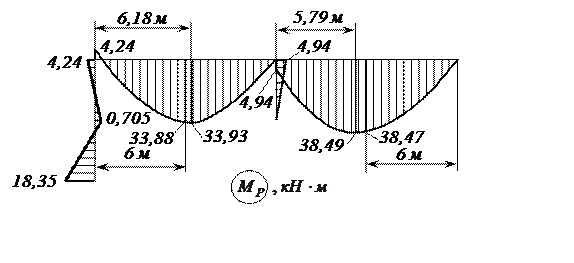
Рис. 24. Окончательная эпюра изгибающих моментов М_Р

8) Выполняем статическую и кинематическую (деформационную) проверки полученной эпюры изгибающих моментов.

Если исходные эпюры  и  построены правильно, т.е. правильно перенесены справочные данные прил. 1 на ОС рассчитываемой рамы, и все дальнейшие вычисления не содержат ошибок, то в методе перемещений достаточной является статическая проверка. Она подтверждает (или не подтверждает, если допущены ошибки) соблюдение условий эквивалентности ЗС и ЭС.

Реакции в дополнительно введенных связях ЭС  будут раны нулю, если узлы и части ЗС находятся в равновесии.

Условия равновесия узлов 2 и 3 с изгибающими моментами, взятыми с окончательной эпюры М_Р (рис. 25), выполняются, что очевидно.

Рис. 25. Проверка равновесия узлов 2 и 3

Соблюдаетсяусловие равновесия и отсечённой части рамы 2-3-4 с поперечными силами в сечениях стоек, найденными по значениям изгибающих моментов М_Р (рис. 26).

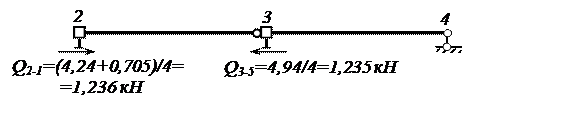
Рис. 26. Проверка равновесия осечённой части рамы 2-3-4

Обратим внимание на то, что в не входят продольные и поперечные силы, а в  не входят продольные силы и изгибающие моменты в стойках, внешняя нагрузка qи реакция опоры 6, поэтому на соответствующих рисунках они не показаны.

Деформационная проверка позволяет обнаружить ошибки, связанные с неправильным изображением исходных эпюр  и  (из-за неправильного представления схем деформирования ОС хотя бы в одном из состояний).

Деформационная проверка выполняется, как известно, перемножением окончательной эпюры М_Р на суммарную единичную эпюру  в любом варианте ОС метода сил (рис. 27).

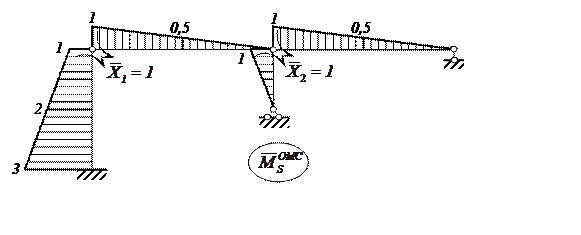
Рис. 27. Суммарная единичная эпюра изгибающих моментов

в ОС метода сил

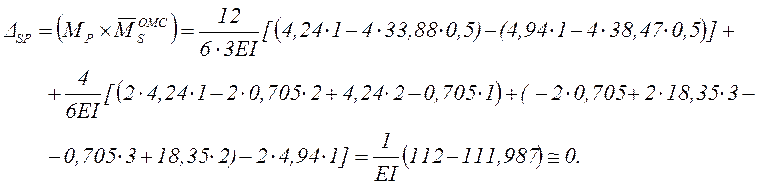
Результаты статической и деформационной проверок показывают, что статическая неопределимость заданной рамы выполнена правильно. Это подтверждается ещё и тем, что такое же решение для этой рамы получено и в методических указаниях «Расчёт статически неопределимых плоских рам методом сил». Там же приведено построение эпюр поперечных и продольных сил и уточнение эпюры М_Р (экстремальные значения на ригелях), поэтому эта часть расчёта здесь не рассматривается.

 

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Дарков, А.В. Строительная механика: учебник для вузов / А.В. Дарков,

Н.Н. Шапошников. – 9-е изд., испр. – СПб. Лань, 2004. – 655 с.

2. Руководство к практическим занятиям по курсу строительной механики: Статика стержневых систем. Учеб. пособие для строит спец. вузов / Под общ. ред. Г.К. Клейна. – 4-е изд., перераб. и доп. – М.: Высш. школа, 1980, – 384 с.

3. Расчёт статически неопределимых плоских рам методом сил: Методические указания к контрольной работе по строительной механике / Сост.: В.С. Симонов, Г.С. Лейзерович. – Комсомсомольск-на-Амуре: ГОУВПО «Комсомольский-на-Амуре государственный технический университет», 2009. – 17 с.

ПРИЛОЖЕНИЕ 1

Реакции и эпюры изгибающих моментов

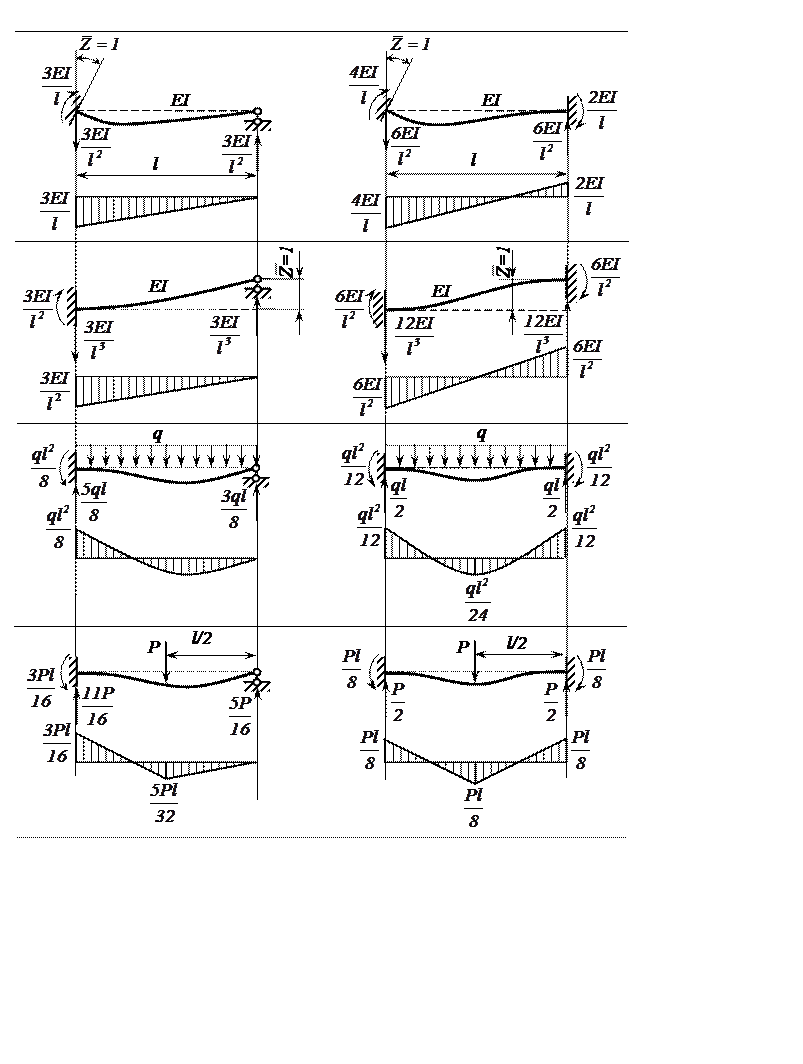
ПРИЛОЖЕНИЕ 2

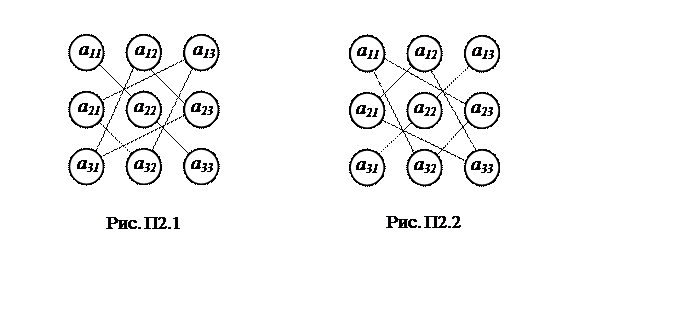
Схема вычисления определителя матрицы третьего порядка

На рис. П2.1 прямыми соединены элементы матрицы, произведение которых входят в определитель со знаком плюс, а на рис. П2.2 прямыми соединены элементы этой же матрицы, произведение которых входит в определитель со знаком минус.

 

Например,

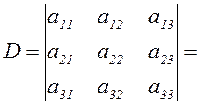
=a₁₁·a₂₂·a₃₃+ a₁₂·a₂₃·a₃₁+ a₁₃·a₂₁·a₃₂ - a₁₂·a₂₂·a_{3 1} - a₁₂·a₂₁·a_{3 3} - a₁₁·a₂₃·a₃₂.