Расчет характеристик системы передачи аналоговых сообщений по цифровому каналу связи, страница 2

                                                                                                                                  (ф.2.8)

                                                                                                              (ф.2.9)

В соответствии с (ф.2.8) и (ф.2.9) получаем значения постоянной состовляющей, мощности переменной составляющей случайного процесса X(t) – (ф.2.10) и (ф.2.11)

                                                                                                                                           (ф.2.10)

                                                                                                                                 (ф.2.11)

Для того, чтобы построить график энергетический спектр случайного процесса X(t) воспользуемся [Л.1 с.119]; изображен на рис. 2.3.

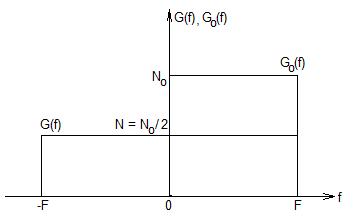
Рис. 2.3. Энергетический спектр случайного процесса X(t)

Аналого-цифровой преобразователь

Для передачи аналогового сигнала по цифровому каналу связи необходимо его преобразование в цифровой поток двоичных символов «0» и «1». Такое преобразование приводит к дискретизации процесса Х(t) с постоянным интервалом Δt (замене непрерывного сигнала x(t) последовательностью отсчетов его мгновенных значений в дискретные моменты времени x(t_i), i = 0, ±1, ±2, …) и квантованию – представлению полученных отсчетов в виде двоичных чисел, разрядность которых определяется заданной точностью.

Интервал дискретизации  определяется на основе теоремы отсчетов [Л.1 стр. 38], расчет его численного значения указан на (ф.3.1)

                                                                                                  (ф.3.1)

Число уровней квантования  L определяется как величина обратная допустимой относительной погрешности (ф.3.2). Заданная погрешность = 0,05%.

                                                                                                                                    (ф.3.2)

Разрядность двоичного представления всей совокупности квантованных уровней находится как ближайшее целое, удовлетворяющее неравенству (ф.3.3); расчет показан на (ф.3.4)

                                                                                                                                                      (ф.3.3)

                                                                                      (ф.3.4)

Расчитаем мощность шума квантования, исходя из свойства его эргодичности и равномерного распределения на интервале (а_макс - а_мин) / 2^k. Тогда мощность будет равна дисперсии случайного процесса X(t), имеющего непрерывное распределение на отрезке [a,b] (ф.3.5)

                                                                                                                         (ф.3.5)

Расчет мощности шума квантования показан на (ф.3.6), его перевод в дБ относительно мощности переменной составляющей на (ф.3.7)

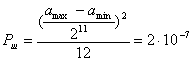                                                                                                             (ф.3.6)

                                                                                                       (ф.3.7)