Расчет характеристик системы передачи аналоговых сообщений по цифровому каналу связи

Санкт-Петербургский Государственный Университет Телекоммуникаций имени профессора М.А.Бонч-Бруевича

Курсовая работа по ТЭС

Вариант № 24

Выполнил: Ермилов И.С.

группа МИ-67

Проверил: Сальников А. П.

Санкт-Петербург, 2008.

Оглавление

Постановка задачи

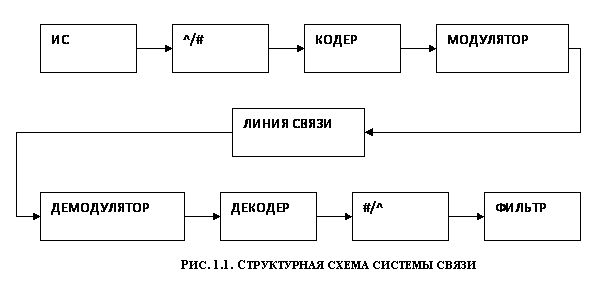
Рассчитать основные характеристики системы передачи аналоговых сообщений по цифровому каналу связи, структурная схема которой приведена на рис. 1.1.

Исходные данные

Предельные уровни аналогового сигнала: а_мин =-1,6В , а_макс  = +1,6В.

Верхняя частота спектра аналогового сигнала F_В = 8 кГц.

Вид модуляции 4-КАМ (четырехуровневая квадратурная амплитудная модуляция).

Источник сообщения

Источник создает непрерывное сообщение Х(t) – случайный квазибелый стационарный эргодический процесс, мощность которого сосредоточена в области частот от 0 до F_В. Мгновенные значения процесса Х(t) равновероятны в интервале от а_мин  до а_макс.

Для отыскания плотности вероятности w(x) нужно исходить из равновероятности мгновенных значений сообщения в интервале Δ = а_макс - а_мин. Внутри этого интервала w(x) определяется из условия нормировки, вне его равна нулю (ф. 1.1).

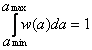,,                                         (ф. 2.1)

Аналитическое выражение функции плотности вероятности приведено на (ф.1.2)

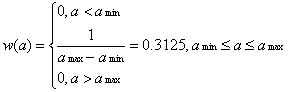                                                          (ф.2.2)

Функция распределения связана с плотностью вероятности интегральным соотношением  [Л.1 стр. 109]. Расчет функции распределения для данного источника сообщения показан на (ф.1.3)

                               (ф.2.3)

На рис. 2.1 и 2.2 показаны функции плотности вероятности и распределения соответственно. Видно, что распределение случайной величины X(t) равномерное.

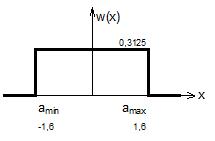
Рис. 2.1. Функция плотности вероятности случайного процесса X(t)

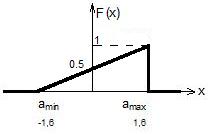
Рис. 2.2. Функция распределения случайного процесса X(t)

Найдем основные характеристики случайного процесса: математическое ожидание по (ф.1.4-1.5) и дисперсию (ф.1.6-1.7).

                                                                                                    (ф.2.4)

,

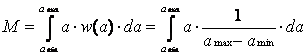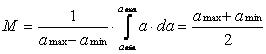                                                                                     (ф.2.5)

                                                               (ф.2.6)

,

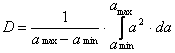
,                                                       (ф.2.7)

Так как процесс эргодический, то из этого следуют равентва (ф.2.8) и (ф.2.9). То есть переменная составляющая случайного процесса равно его математическому ожиданию, а мощность переменной составляющей – его дисперсии.