Моделирование электромагнитных переходных процессов на ЭВМ: Методические указания к лабораторным работам, страница 6

                                                                                     Таблица 1.2 – Исходные данные

№ варианта	, Ом				L, Гн
	i=1	i=2	I=3	i=4
1	0	1	2	3	0,05
2	0	1	2	5	0,1
3	0	1	2	5	0,09
4	0	2	10	20	0,7
5	0	0,4	1	2	0,04
6	0	1	2	5	0,09
7	0	1	2	4	0,06
8	0	1	2	3	0,04
9	0	1	2	3	0,06
10	0	1	2	3	0,06

                                                                        Таблица 1.3 – Результаты исследований

Ri
i=1…4

ЛАБОРАТОРНАЯ РАБОТА  № 2

МОДЕЛИРОВАНИЕ НА ЭВМ ПРОЦЕССА ВНЕЗАПНОГО МЕТАЛЛИЧЕСКОГО ТРЕХФАЗНОГО КОРОТКОГО ЗАМЫКАНИЯ

Цель работы. Исследовать процесс внезапного металлического трехфазного                     

                        короткого замыкания в активно-индуктивной цепи.

                                       Пояснения к работе.

     Процесс трехфазного металлического короткого замыкания рассмотрим в простейшей электрической системе (рис. 2.1) [2,5]. Пусть питание системы осуществ­ляется от источника бесконечной мощности с сопротивлением равным нулю.

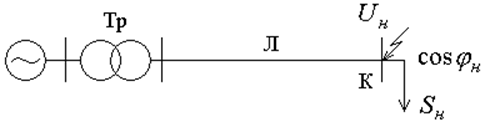                    Рис.2.1 – Исследуемая электрическая система

      На рис. 2.2 приведена схема замещения рассматриваемой системы. Па­раметры схемы замещения для разных вариантов, приведенные к номинальному напряжению в месте КЗ –Uн, све­дены в табл. 2.1.

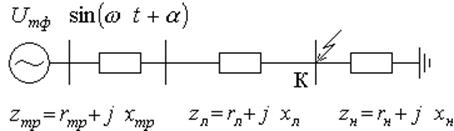         Рис.2.2– Схема замещения исследуемой электрической системы

     Ток, протекавший в этой цепи перед коротким замыканием, называ­ется предшествующим. Например, предшествующий ток фазы А можно определить по формуле

        .                           (2.1)

Здесь 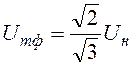 – амплитуда фазного напряжения;

            – амплитуда фазного тока;

            – угловая частота сети;

          – полное сопротивление системы;

           – активное сопротивление системы;

          – реактивное сопротивление системы;

           – угол сдвига между током и напряжением.

     Пусть в точке K (рис. 2.2) на шинах произошло трехфазное короткое замыкание. Как правило, в месте короткого замыкания возникает электрическая дуга, сопротивление ко­торой  необходимо учесть в сопротивлении цепи короткого замыка­ния. Рассмотрим металлическое короткое замыкание, при этом сопро­тивление дуги  [2]. Дифференциальное уравнение переходного про­цесса, возникающего при коротком замыкании, например, для фазы А можно записать в следующем виде:

                                               (2.2)

Решением этого уравнения является выражение  [2]       

      ,                        (2.3)

где ,  - периодическая и апериодическая составляющие тока;

      – амплитуда периодической составляющей тока;

       – постоянная времени апериодической составляющей

                                              тока;

       – полное сопротивлений цепи oт точки питания до точки

                                    замыкания (цепи КЗ);

        – активное сопротивление цепи КЗ;

        – реактивное сопротивление цепи КЗ;

        – угол сдвига между током и напряжением в цепи КЗ;

         – начальное значение апериодической составлявшей тока;

        – индуктивность цепи КЗ:

         – фаза напряжения при  времени .

     По первому закону коммутации (ток в индуктивной цепи скачком изме­ниться не может [1]) запишем

            или          .

Отсюда находим начальное значение апериодической составляющей тока

                     .                              (2.4)

На рис. 2.3 показаны зависимость  и ее составляющие.