Моделирование электромагнитных переходных процессов на ЭВМ: Методические указания к лабораторным работам, страница 2

           На   рис. 1.4  показана форма тока,  соответствующая  зависимости   и   построенная по кривой намагничивания. Видно (рис 1.4), что  зависимость    сильно отличается от   синусоиды,   особенно   в   начальной стадии переходного процесса. Это   происходит потому,   что при  насыщении   сердечника   индуктивность становится нелинейной и  вызывает  возникновение нелинейного тока. Нелинейный ток можно   разложить  на  высшие  гармоники. (В  курсе ”Электромагнитные  переходные  про-цессы”  разложение  тока  на  высшие   гармоники не  рассматривается. Однако в последние  годы  в электроэнергетике  стали   уделять   большое внимание   вопросам  качества   электроэнергии  и  студенты  должны  знать, что индуктивное сопротивление трансформатора при  насыщении  становится   нелинейным,  а  нелинейное сопротивление  можно рассматривать как генератор высших гармоник [1], ко-торое приводят к искажению синусоидальной формы тока и напряжения и, следовательно, ухудшение качества  электроэнергии. Данная  лабораторная  работа  очень  удобна  для  знакомства  с  этим вопросом, полученные  сведения будут  использованы  в  курсах  ”Электроснабжение  промышленных  предприятий”,  ”Изоляция  и  перенапряжения   в  СЭС”  и  других).

           Разложим  ток    на  высшие   гармоники. Из  курса математики  известно,  что любую периодическую  функцию y=f(x),  удовлетворяющую  условиям  Дирихле,  можно  разложить  в ряд  Фурье,  а,  как  известно,  все  периодические    функции  электротехники  условиям  Дирихле  удовлетворяют [1].  В общем  виде  разложение  функции  y=f(x)  в  ряд  Фурье можно   представить  так  [1]:

                     (1.7)

 Здесь   - постоянная  составляющая;   -амплитуда  основной  (первой)  синусной  гармоники ; -амплитуда  высшей (k-й)  синусной  гармоники ; - амплитуда основной  (первой) косинусной  гармоники;  - амплитуда  высшей  (k-й)  косинусной   гармоники .

     Если  периодические кривые  обладают симметрией   того  или  иного  вида , то  некоторые  коэффициенты  в  разложении в  ряд  Фурье (1.7)  обращаются  в  нуль [1].  Так,  если  кривая  симметрична  относительно оси ординат ,то в разложении  в  ряд Фурье отсутствуют следующие коэффициенты:   - и  оно принимает  вид :

              (1.8)

      Амплитуды  постоянной составляющей   и  гармоник  определяются  по формулам  [1]

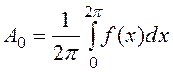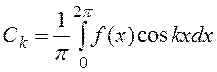            и                         (9.1)

  Коэффициенты  ряда  Фурье  по  известной  кривой    y=f(x)  можно   определить графическим  методом  [1],  основанным  на  замене определенных  интегралов  (1.9)  суммами  конечного  числа  слагаемых. С  этой  целью  период  функции   f(x),  равный  , разбивается  на   n равных  частей   и  интегралы  заменяются   суммами:

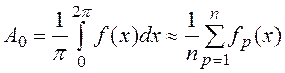
     и

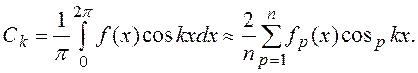                                       (1.10)

     Здесь  p - текущий индекс,  он  принимает  значение  1….n; - значение функции f(x)  в  середине   p-го   интервала;  - значение  функции    в середине  p-го  интервала .

     Однако  ток  холостого  хода  трансформатора   во  время переходного  процесса  в  общем  случае  периодической  функцией   не  является,  поэтому, строго говоря,  его  разложить  на   гармоники   нельзя. Вместе с тем, рассматривая переходный процесс за один период можно считать функцию квазипериодической. Это после разложения кривой тока на высшие гармоники позволяет определить действующее значение тока и тепловой импульс за первый период [3].   Иное  дело – ток  в  цепи  при   r=0 .  В  этом  случае  функция    будет  периодической  и  симметричной  относительно  оси  ординат  (рис 1.5).

      Ряд  Фурье  для  тока  намагничивания    при   r=0 принимает  вид:

                             (1.11)

где  -постоянная  составляющая ;  -амплитуда  k-й  косинусной  гармоники

     В лабораторной  работе  при  определении  постоянной  составляющей  и амплитуд  косинусных  гармоник  период разбивается на  48  частей ,  и  они  определяются  по  формулам : 

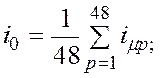
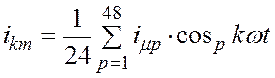                                                     (1.12)

 где   - значения  тока     в  середине   р-го  интервала;

  - значение  функции     в  середине  р-го  интервала.