Моделирование электромагнитных переходных процессов на ЭВМ: Методические указания к лабораторным работам

                              МОДЕЛИРОВАНИЕ    

ЭЛЕКТРОМАГНИТНЫХ ПЕРЕХОДНЫХ

ПРОЦЕССОВ НА ЭВМ

Омск 2006

 Федеральное агентство по  образованию

Государственное образовательное учреждение

 высшего профессионального образования

«Омский государственный технический университет»

                              МОДЕЛИРОВАНИЕ    

ЭЛЕКТРОМАГНИТНЫХ ПЕРЕХОДНЫХ

ПРОЦЕССОВ НА ЭВМ

Методические указания

к лабораторным работам

Омск – 2006

               .

Cоставители: Шкаруба Михаил Васильевич,

                        Эрнст Александр Дмитриевич

ЛАБОРАТОРНАЯ РАБОТА  №1

МОДЕЛИРОВАНИЕ  НА ЭВМ  ХОЛОСТОГО  ХОДА

ТРАНСФОРМАТОРА

   Цель работы: Исследовать переходный процесс, возникающий при включении 

                           однофазного трансформатора с разомкнутой вторичной   обмот-

                           кой   под синусоидальное напряжение.

                                                   Пояснения к работе.

     Рассматриваемый процесс включения однофазного трансформатора с разомкнутой первичной обмоткой (рис.1.1) полностью идентичен процессу включения катушки с ферромагнитным сердечником  под синусоидальное напряжение и описывается уравнением [1]

                               ,                                   (1.1) 

где Um - амплитуда синусоидального напряжения; a - фаза напряжения при  t=0  (фаза включения);  - потокосцепление первичной обмотки;  n₁ - число  витков  первичной  обмотки;  Ф – магнитный поток;  - мгновенное значение тока холостого хода;   r - активное сопротивление первичной обмотки.

Предполагается, что магнитная характеристика трансформатора (характеристика холостого хода)  известна  (рис. 1.2). Так как магнитная характеристика нелинейна, то и дифференциальное уравнение (1.1) будет нелинейным.

            Решить это дифференциальное уравнение можно, например, методом условной линеаризации [1], который заключается в следующем. Пусть второе слагаемое в первой части уравнения (1.1) мало по сравнению с первым. Такое условие соблюдается, например, при включении мощных трансформаторов с разомкнутой вторичной обмоткой, так как активное сопротивление  r  у них  обычно незначительно. Поэтому второе слагаемое   имеет второстепенное значение по  сравнению   с членом   и  неточность его вычисления существенно  не повлияет  на определение  параметров переходного процесса.

      Зависимость  является нелинейной, так как L  есть функция  ,  но в данном  случае можно приближенно  принять  L=const,  и связь между  и   становится  линейной:                                                      

                                                                                                              (1.2)

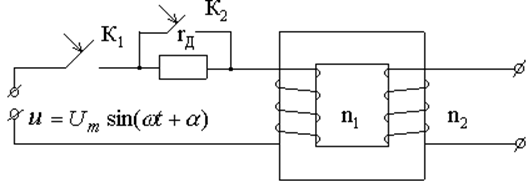                Рис.1.1– Исследуемая  схема  включения   однофазного  трансформатора

                      

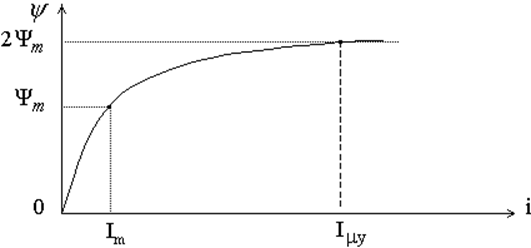                 Рис.1.2 – Магнитная  характеристика   трансформатора

 

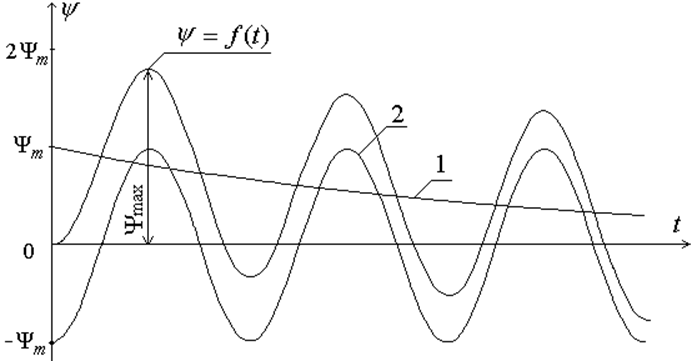                    Рис. 1.3 –  Кривая    и  ее  составляющие:

                                1 – апериодическая   ;  2 – периодическая     

          Отсюда можно выразить   и подставить   в  уравнение  (1.1). Тогда уравнение  (1.1)  примет  вид

                   .                               (1.3)

       Уравнение (1.3) становится  линейным  и  имеет решение

                                                                  (1.4)

      где     - амплитуда потокосцепления; (a – j)  – фаза включения потокосцепления;  угол  .

         Так как r<<(),  угол . Максимум потокосцепления соответствует фазе включения  напряжения     и  определяется   уравнением

                   ,                          (1.5)         

так  как в этом случае  .  На  рис. 1.3  приведена  зависи–мость  и  ее  составляющие –  и  .  Макси-мальное мгновенное значение потокосцепления   имеет место через поло–вину периода и  при f =50 Гц  можно  записать

                                                          (1.6)

      Из выражения (1.6) следует, что при большой постоянной времени  максимальное значение потокосцепления равно примерно , а ударный  коэффициент  [2] .    

                На рис. 1.2 приведена магнитная  характеристика трансформатора. В установившемся режиме работы трансформатора амплитудное значение потокосцепления  находится вблизи колена магнитной характеристики. Этому значению  потокосцепления  соответствует наибольшая  по величине  амплитуда тока , но при включении трансформатора амплитуда потокосцепления превышает   (рис. 1.3), рабочая точка  переходит  в  область насыщения  кривой намагничивания,  что  приводит  к  очень большим  броскам тока  намагничивания.