Энергетический спектр электронов в кристалле. Волновая функция и ее свойства. Уравнение Шредингера для свободной частицы

Лекция 5

Энергетический спектр электронов в кристалле

Классическая релятивская физика (Ньютон)	Классическая релятивская физика (Эйнштейн)
Квантовая нерелятивская физика	Физика элементарных частиц

Носит характер вероятности

Принципы квантовой физики
Классическая физика		Квантовая физика

Принцип дополнительности Бора

Если есть частица массой m и обладающая скоростью, то с позиции квантовой физики ей сопоставляется волна:

;         ;                         

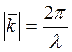
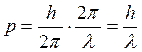
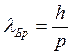, если соотношение Де Бройля и параметр среды , то частица ведет себя неопределенно.

Волновая функция и ее свойства

- волна Де Бройля ее физический смысл связан с вероятностью.

- условие волновой функции

;

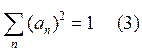
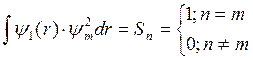, где S-функция Дирака (6)

Оператор импульса  где

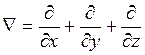
Оператор кинетической энергии 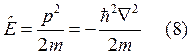, где

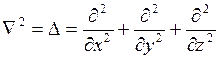
Оператор потенциальной энергии

Оператор полной энергии

Уравнение Шредингера: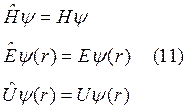

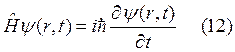
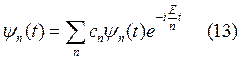
Свойства:

1. Линейность
2. Самосопряженность  
3. 

4. 

5. Коммутативность ,

 ,

6. ;L-собственное значение оператора L, собственная функция оператора
7. Для эрмитовских операторов вещественно.

Если волновая функция  непрерывная, то любое воздействие на нее определено в последующие моменты времени, то есть, определено производной. Стационарное уравнение Шредингера не зависит от времени.

Уравнение Шредингера для свободной частицы

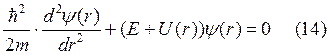, а так как   

;                         

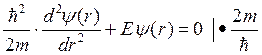
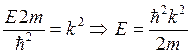
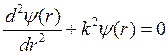
Волна Де Бройля – это волновая функция которая описывает свободную частицу.

Потенциальная яма

 

,

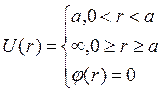Внутри ямы справедлива формула