Взаимодействие электронов и фононов

Лекция 17

Итак, мы с вами теперь имеем два случая: низких температур – температура меньше чем температура Дебая, и случай высоких температур – температура больше температуры Дебая. И в силу математических трудностей, здесь есть своеобразная процедура. Процедура такая: во-первых введем безразмерные переменные, но сейчас это неудобно, поэтому вводится безразмерная переменная по соотношению:   итак это безразмерная энергия. И тогда для средней энергии после перехода к новым координатам будем иметь: 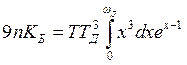 и для теплоемкости: 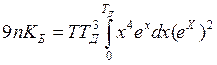.Эти два интеграла можно привести к простому решению выбирая либо низкую, либо высокую температуру. Рассмотрим сначала случай высоких температур:  - тогда х малая величина, тогда e^x раскладывается в ряд по степеням малого параметра: .И тогда интеграл для теплоемкости получается следующим: 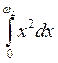, решая этот интеграл получаем для теплоемкости в случае высоких температур – прямо закон Делонга. Для случая низких температур придется рассмотреть средние температуры, так как при низких температурах нельзя раскладывать в ряд, но при условии, что верхней предел мы делаем бесконечностью. В случае низких температур нижний предел стремится к бесконечности, и наше приближение стремится к истинному значению и мы получаем формулу Дебая.

Взаимодействие электронов и фононов.

Фонон-фононное рассеивание.

Данное рассевание невозможно объяснить, используя  гармоническое приближение. Необходимо вспомнить понятие ангормонизма??? – разложение потенциальной энергии в ряд Тейлора. Мы имеем два фонона, то есть у нас есть две волны. Рассматриваем как всегда одномерный случай. Уравнение волн:  и . Дальше процедура следующая: мы должны найти возвращаю силу, действующую на какой либо атом со стороны. Или вернее найти возвращаю силу, действующую при возвращении атома на место при воздействии на него двумя фононами, то есть двумя волнами. Сила F будет определяться как сила связанная с первым и вторым фононом. В результате такого рассмотрения мы получим при совместном взаимодействии двух фононов:  и  . Эти фононы будут отличаться от исходных частотами и волновыми векторами. \\ПРОЗРАЧКА\\

В k пространстве достаточно рассмотреть сферу Дебая – плоское сечение сферы Дебая. И у нас есть два фонона, которые характеризуются двумя точками внутри этой сферы: k₁ и k₂. Дальше они начинают взаимодействовать, то есть по закону сохранения мы должны найти k₃=k₁+k₂ – векторное сложение. В зависимости от того, чему равна величина вектора k₃ после взаимодействия мы и различаем два случая: |k₃|<k_дебая – нормальный процесс и когда k<sup>`</sup><sub>3</sub>>k<sub>дебая</sub>, k`₃ есть сумма k₃+k_дебая – процесс переброса. Физические смысл – тепловое сопротивление - нелинейный процесс. То есть первое что нужно знать, это что при процессах взаимодействия должны выполняться законы сохранения. Ну а теперь рассмотрим время релаксации – время свободного пробега -  - вероятностная величина. Время свободного пробега обратно пропорционально числу рассеивающих центров. Если мы хотим оценить фонон-фононное рассеивание мы должны оценить сколько этих фононов возбуждено при разной температуре. А ответ нам дает статистика Планка. Поэтому дальше все очень просто – использована статистика планка для определения числа фононов. То если мы запишем статистику планка: .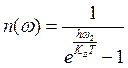

Итак качественное рассмотрение здесь связано с простым выражением когда можно единицу рассмотреть, а когда нельзя. И второй случай – когда экспоненту можно разложить в ряд, а когда нельзя. То есть когда показатель степени мал, мы раскладываем  по степеням свободы. То есть когда температура высокая мы можем спокойно разложить экспоненту в ряд и получаем закон равного распределения по степеням свободы при высоких температурах Максвелла-Больцмана. При низких температурах фононы обладают малой частотой и малым волновым вектором, и как следствие большой длиной волны. По этому при низких температурах рассматривают взаимодействие фононов с препятствиями, то есть с дефектами, как явления такие же как и в волновых процессах, то есть оптические волны, рассеивающиеся на препятствиях, то есть дифракция преломление и т.д. А вот на высоких температурах, там где действительно длинна волны фонона мала мы переходим к рассмотрению упругого взаимодействия.