



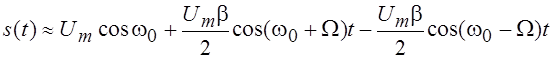 .
.
Следует заметить, что такой же амплитудный спектр имеет амплитудномодулированное колебание с гармоническим законом модуляции. Убедиться в этом мы предлагаем читателю.
С ростом индекса модуляции число отличных от нуля гармоник растет и спектр колебания расширяется. Так как высокое качество ЧМ передач можно обеспечить при больших индексах модуляции, то становится понятным, почему качественное стереовещание ведется в УКВ диапазоне, а не на длинных и средних волнах.
6.6. Функции гипергеометрического типа
При знакомстве с классическими ортогональными полиномами, мы отмечали, что они являются решениями соответствующих линейных дифференциальных уравнений второго порядка:
![]() ,
,
где ![]() и
и ![]() – полиномы порядка не выше второго,
– полиномы порядка не выше второго, ![]() – собственные значения, соответствующие
– собственные значения, соответствующие ![]() . Так, для полиномов Лежандра
. Так, для полиномов Лежандра ![]() это уравнение имеет вид
это уравнение имеет вид ![]() , для полиномов Лаггера
, для полиномов Лаггера ![]()
![]() , а для полиномов
Эрмита
, а для полиномов
Эрмита ![]()
![]() .
.
Дифференциальное
уравнение гипергеометрического типа является обобщением уравнения для
классических ортогональных полиномов и записывается следующим образом ![]() , где a, b, c – произвольные числа,
причем
, где a, b, c – произвольные числа,
причем ![]() . Это уравнение иногда называют
дифференциальным уравнением Гаусса, а его решения функциями Гаусса. Одно из
решений этого уравнения, называемое гипергеометрической функцией, имеет вид
. Это уравнение иногда называют
дифференциальным уравнением Гаусса, а его решения функциями Гаусса. Одно из
решений этого уравнения, называемое гипергеометрической функцией, имеет вид
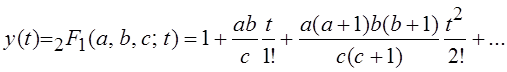
Ряд, определяющий эту
функцию, называется гипергеометрическим рядом. Входящие в коэффициенты ряда
произведения ![]() обозначают как
обозначают как ![]() . Индексы 2 и 1, входящие в обозначение
функции
. Индексы 2 и 1, входящие в обозначение
функции ![]() , показывают, что два параметра (a и
b) входят в числитель коэффициентов, а один (c) – в знаменатель.
, показывают, что два параметра (a и
b) входят в числитель коэффициентов, а один (c) – в знаменатель.
Если a или b
равно отрицательному целому числу, то ряд обрывается и ![]() превращается
в полином степени
превращается
в полином степени ![]() .
.
С помощью признака Даламбера можно установить, что радиус сходимости гипергеометрического ряда равняется единице.
Укажем элементарные свойства гипергеометрической функции.
Прежде всего, отметим
симметрию ![]() по отношению к параметрам a и b.
по отношению к параметрам a и b.
Дифференцируя гипергеометрический ряд почленно, получим:
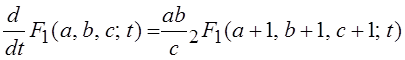 ,
,
или, в общем случае:
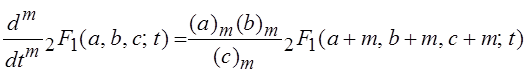 .
.
Гипергеометрические функции удовлетворяют большому количеству рекуррентных соотношений типа
![]() ,
,
с которыми можно познакомиться с помощью справочников по теории специальных функций [15].
Придавая параметрам a, b и c конкретные значения, можно получить представления различных функций через гипергеометрическую.
1. Элементарные функции
Выше отмечалось, что при
отрицательных целых значениях параметра a или b гипергеометрическая
функция превращается в полином. Если a = 1/2, b = c = 1, то 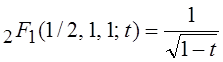 .
.
Для логарифмической
функции выполняется соотношение ![]() , а для обратных
тригонометрических функций
, а для обратных
тригонометрических функций ![]() ,
, ![]() .
.
Во многих задачах
приходится сталкиваться с эллиптическими интегралами первого ![]() и второго
и второго ![]() рода,
под которыми понимают интегралы следующего вида:
рода,
под которыми понимают интегралы следующего вида:
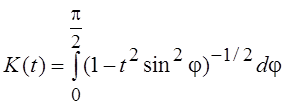 ;
; 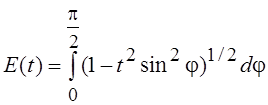 .
.
Если положить a = b =
1/2, c = 1 и ![]() , то
, то 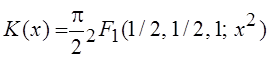 ,
аналогично при a = –1/2, b = 1/2, c = 1 и
,
аналогично при a = –1/2, b = 1/2, c = 1 и ![]() ,
, 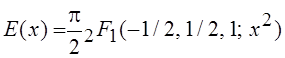 .
.
Рассмотренные выше
классические ортогональные полиномы также выражаются чрез гипергеометрическую
функцию. Так, полином Лежандра представляет собой 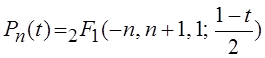 , а
полином Чебышева первого рода
, а
полином Чебышева первого рода 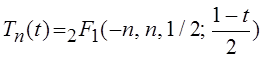 .
.
Вырожденная
гипергеометрическая функция ![]() определяется рядом
определяется рядом
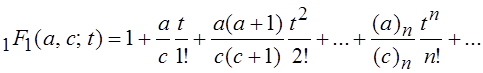 ,
,
где, как и раньше, a и c
– любые числа, кроме ![]() . В отличие от гипергеометрической
функции данный ряд сходится при любых конечных t. Вырожденная гипергеометрическая
функция является решением уравнения Куммера
. В отличие от гипергеометрической
функции данный ряд сходится при любых конечных t. Вырожденная гипергеометрическая
функция является решением уравнения Куммера
![]() .
.
Правила дифференцирования
![]() аналогичны правилам для
аналогичны правилам для ![]() , т. е.
, т. е.
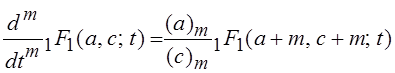 .
.
То же можно сказать и о рекуррентных
соотношениях, связывающих функцию ![]() с двумя любыми
смежными функциями
с двумя любыми
смежными функциями ![]() и
и ![]() , т. е.
, т. е.
![]() ;
;
![]() .
.
Более подробно с рекуррентными соотношениями для вырожденных гипергеометрических функций можно познакомиться с помощью справочников.
Для приложений оказываются полезными формулы, связывающие вырожденные гипергеометрические функции с положительным и отрицательным значением аргумента:
![]() .
.
При некоторых значениях
параметров a и c функцию ![]() можно
выразить через другие функции. Так например,
можно
выразить через другие функции. Так например, ![]() , где т
– целое число,
, где т
– целое число, 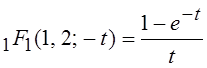 , при a = –k, c = 1/2,
, при a = –k, c = 1/2, ![]() :
:
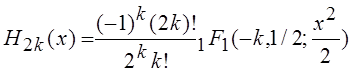 ,
,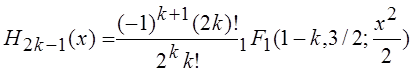 ,
,
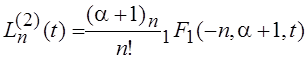 .
.
Часто встречающийся в приложениях интеграл вероятностей
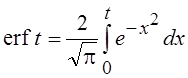
также может быть представлен с помощью вырожденной гипергеометрической функции
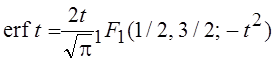 .
.
И, наконец, функции Бесселя также
могут быть выражены через ![]() следующим образом:
следующим образом:
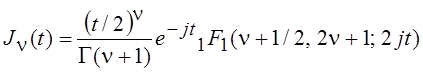 ;
; 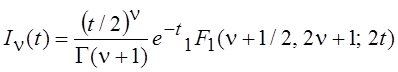 .
.
С примерами использования гипергеометрических функций мы встретимся в разделе, посвященном случайным процессам.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.