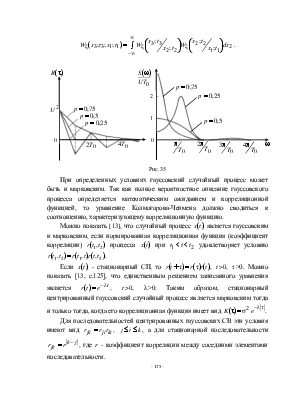
Марковские процессы как класс случайных процессов

Глава 8. Марковские процессы

Марковские процессы составляют весьма важный класс случайных процессов, давая возможность описывать многочисленные явления, встречающиеся в науке и технике. Как уже отмечалось выше, привлекательность марковских процессов связана с возможностью получить полное статистическое описание на основе ПВ не выше второго порядка. Это связано с тем, что для любых t₁ < t₂ < t₃ при фиксированном значении процесса в момент t₂, случайная величина x₃ = x(t₃) не зависит от того, какое значение принял процесс в момент t₁, т. е.

.

Поэтому многомерная ПВ марковского процесса имеет вид

.

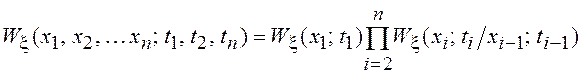В соответствии с общей классификацией случайных процессов, введенной ранее, марковские процессы с дискретными состояниями и дискретным временем называют цепями Маркова в честь русского математика А.А. Маркова; марковские процессы с дискретными состояниями и непрерывным временем называют дискретными марковскими процессами. Аналогично общей классификации определяются марковская последовательность (непрерывное состояние и дискретное время) и непрерывнозначный марковский процесс.

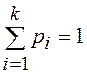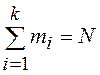Начнем наше знакомство с марковскими процессами с цепей Маркова. Марковские цепи являются обобщением схемы независимых испытаний, в которой вероятности состояний   не зависят от того, в каком состоянии окажется система S в результате предыдущего испытания и не зависят от номера испытания. Вероятности того, что в результате N испытаний система m_i раз оказывалась в состоянии s_i ( и ) определяется мультиномиальным распределением, с которым мы познакомились выше. При k = 2 мы получаем биномиальное распределение вероятности.

Для марковской цепи (простой марковской цепи) вероятность оказаться в состоянии s_i  в l-м испытании является условной и зависит от того, в каком состоянии система оказалась в результате l – 1-го испытания и не зависит от исходов, предшествовавших l – 1-му испытанию. Классическим примером марковской цепи является задача перемещения (блуждания) частицы по прямой под действием сил, смещающих частицу на единицу перемещения вправо с вероятностью р и влево с вероятностью q = 1 – p. Ясно, что вероятность оказаться в точке с координатой k для частицы, находящейся после предыдущего испытания в точке с координатой l равна нулю, если ; р, если k – l =1; q, если k – l = –1 и не зависит от того, как частица попала в точку с координатой l.

Рассмотрим более подробно однородные цепи Маркова, для которых условная вероятность для системы оказаться в т-ом испытании в состоянии s_j при условии, что она находилась в состоянии s_i, т. е.  не зависит от номера испытания т. Эту вероятность для краткости будем обозначать как  и называть переходной вероятностью. Обратим внимание на то, что первый индекс указывает, в каком состоянии находилась система, а второй – куда она перешла в результате испытания.

Полное вероятностное описание однородной марковской цепи дает вектор начальных вероятностей , определяющий вероятность пребывания системы в состоянии s_i, i = 1, 2, …, k до начала испытаний и матрица перехода за один шаг (в результате одного испытания) , где вероятности перехода p_ij  были определены выше. Так как в результате испытания система перейдет в  одно из k состояний (вероятности p_ii, стоящие на диагонали матрицы Р₁, дают вероятности того, что система, находясь в состоянии s_i,  там и остается), то по условию нормировки 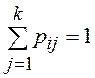, i = 1, 2, …, k. Таким образом, сумма элементов каждой строки матрицы Р₁ равна единице.

Пусть система находится в состоянии s_i, i = 1, 2, …, k и нам надо найти вероятности перехода через п испытаний p_ij(п). Рассмотрим промежуточные испытания с номером 0 < m < n. В этом испытании система окажется в одном из возможных состояний . Вероятность такого перехода в соответствии с введенными обозначениями будет равна . Вероятность же перехода из состояния s_r в s_i за оставшиеся п – т будет равна p_rj(n – m). На основании формулы полной вероятности (переход в состояние j может происходить через любые состояния 1 £ r £ k) получим:

.

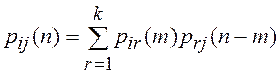Если обозначить через Р_m и P_n–m  матрицы перехода за т и п – т шагов соответственно, и учесть приведенное выше выражение для , можно записать, что Р_n = P_mP_n–m, 0 < m < n. При п = 2, т = 1, п – т =1 и
. Аналогично, , а в общем случае .

Если начальные состояния системы  определяются вектором , то вероятности состояний  после п шагов будут равны .

Представляет интерес поведение матрицы Р_п с ростом п. Справедлива следующая теорема. Если при некотором  s> 0 все элементы матрицы перехода Р_s положительны, то существуют такие постоянные числа p_j, j = 1, 2, …, k, что независимо от индекса i имеют место равенства . Вероятности, определяемые вектором 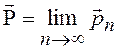, называются финальными.

Смысл полученного результата важен и прост. В условиях справедливости данной теоремы вероятности системы находиться в состояниях  по истечении большого числа переходов (п ®¥) не зависят от того, в каком она состоянии находилась в начале. Финальные вероятности должны удовлетворять системе k линейных уравнений .