Марковские процессы как класс случайных процессов, страница 2

Эта теорема, доказанная А.А. Марковым, явилась первой в ряду эргодических теорем, играющих важную роль в науке и технике.

В качестве примера рассмотрим однородную марковскую цепь с двумя состояниями, под которыми будем понимать решения обнаружителя об отсутствии сигнала на входе  и его наличии . Априорные вероятности отсутствия и наличия сигнала задаются вектором , а матрица одношаговых вероятностей перехода равна

,

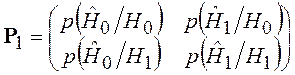или в принятых в статистической теории радиотехнических систем обозначениях (см. [11]).

,

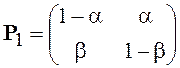где a – вероятность ложной тревоги, b – вероятность пропуска сигнала. Пользуясь методикой отыскания финальных вероятностей [12], получим 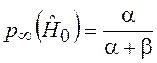 и 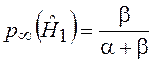 – вероятности состояния обнаружителя после п ®¥ шагов. Как и должно быть, .

Заметим, что мы рассмотрели случайные блуждания обнаружителя. При оптимальной организации его работы при п ®¥ условные вероятности  и  стремятся к нулю, если , где q₀ – параметр обнаружения при однократном наблюдении.

В качестве второго примера рассмотрим квазислучайный телеграфный сигнал, т. е. процесс, принимающий лишь два значения U_m и – U_m, причем изменения состояния происходят в фиксированные моменты времени , где t₀ – случайная величина, равномерно распределенная на отрезке [0, T], а Т – фиксированный временной интервал, п = 0, 1, 2, … – целые неотрицательные числа. Вероятности изменения состояния в моменты времени t_n определяются матрицей перехода

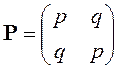, p+ q = 1.

В силу симметрии матрицы Р марковская цепь называется симметричной.

На рис. 34 приведена реализация такого процесса при .

Можно показать [12], что рассматриваемый процесс будет стационарным, если начало координат не совмещать с моментом возможного изменения состояния. Его корреляционная функция при  будет иметь вид

.

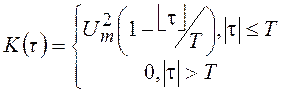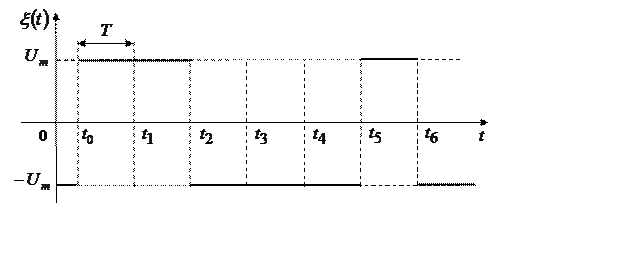
Рис. 34

Выражение для СПМ соответствующее произвольным значениям  и приведены ниже

.

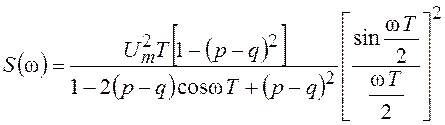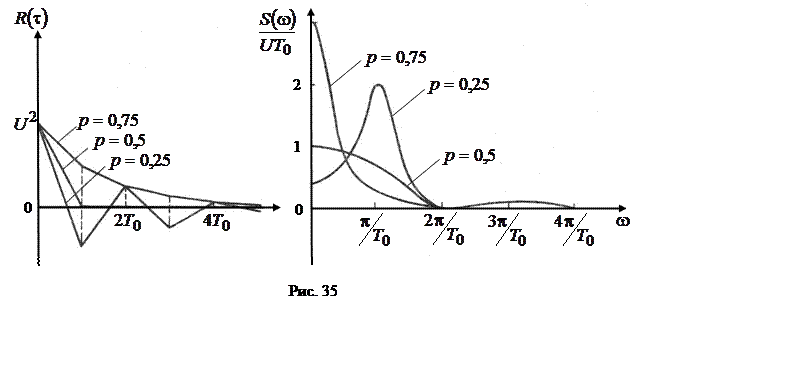
На рис. 35 приведены графики КФ и СПМ при различных значениях  и . Как и следовало ожидать, наиболее широкополосным процесс будет при =0,5.

Напомним, что условие факторизации многомерной ПВ, т.е. представления ее в виде 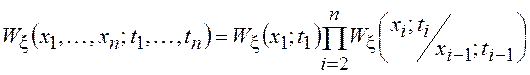, является определением Марковского процесса. Условные ПВ 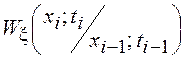 помимо условий неотрицательности и нормировки 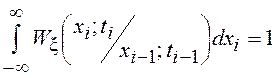 должны также удовлетворять интегральному уравнению Колмогорова-Чепмена, называемому иногда уравнением Смолуховского, утверждающему, что для любых

.

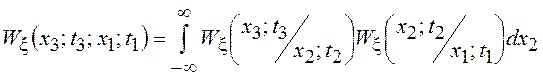При определенных условиях гауссовский случайный процесс может быть и марковским. Так как полное вероятностное описание гауссовского процесса определяется математическим ожиданием и корреляционной функцией, то уравнение Колмогорова-Чепмена должно сводиться к соотношению, характеризующему корреляционную функцию.

Можно показать [13], что случайный процесс  является гауссовским и марковским, если нормированная корреляционная функция (коэффициент корреляции)  процесса  при  удовлетворяет условию .

Если  - стационарный СП, то , >0, >0. Можно показать [13, с.125], что единственным решением записанного уравнения является , >0, >0. Таким образом, стационарный центрированный гауссовский случайный процесс является марковским тогда и только тогда, когда его корреляционная функция имеет вид .

Для последовательностей центрированных гауссовских СВ эти условия имеют вид , , а для стационарной последовательности , где  - коэффициент корреляции между соседними элементами последовательности.

Решение уравнения Колмогорова-Чепмена позволяет найти вид ПВ 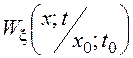, >. Однако его решение в общем случае представляет собой чрезвычайно сложную задачу. Для частного случая марковских процессов, называемых диффузионными, интегральное уравнение Колмогорова-Чепмена удается свести к дифференциальному уравнению в частных производных вида

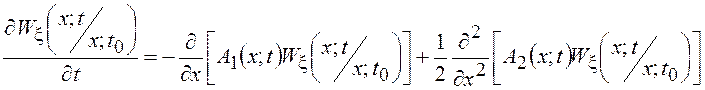,  (8.1)

которое называется прямым уравнением Колмогорова или уравнением Фоккера-Планка. В приведенном уравнении

,

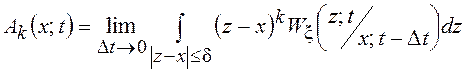причем при  .  и  называются соответственно коэффициентом сноса и коэффициентом диффузии. Уравнение (8.1) является линейным дифференциальным уравнением в частных производных и относится к параболическому типу. Решение уравнения должно удовлетворять следующим условиям:

·  оно должно быть неотрицательным;

·  подчиняться условию нормировки;

·  удовлетворять начальному условию =.

В ряде задач значение марковского процесса в начальный момент времени  не фиксировано, как выше, а подчиняется ПВ .

Можно показать [9], что одномерная ПВ диффузионного марковского процесса для произвольного момента времени удовлетворяет уравнению

=

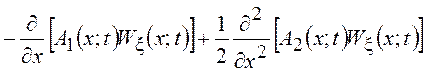
Для решения этого уравнения необходимо кроме начальных условий, о которых шла речь при обсуждении уравнения (8.1), задать граничные условия которые могут быть весьма разнообразными и определяются особенностями решаемой задачи. Подробнее с этой проблематикой можно познакомиться в [12].