Линейные операторы и функционалы. Часть 3, страница 3

1.  Потребуем, чтобы малым изменениям исходного сигнала s(t) соответствовали бы малые изменения огибающей S(t) и фазы Ф(t). Так как функции определяющие  S(t) и  Ф(t) непрерывны, то сформулированное требование означает непрерывность оператора А.

2.  Фаза, а, следовательно, и мгновенная частота не должны зависеть от энергии (нормы) сигнала. Это означает, что оператор А должен быть однородным, т. е. .  В этом случае

.

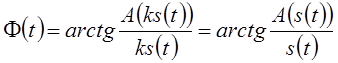3.  Для гармонического сигнала s(t) = U_m cos (w₀t + j) мы должны получить S(t) = U_m  и Ф(t) = w₀t + j. Это означает, что А[U_mcos(w₀t + j)] =
= U_msin (w₀t + j).

В [11] доказано, что единственным линейным оператором, удовлетворяющим этим условиям, является оператор Гильберта. Следовательно, определенные на его основе понятия огибающей и фазы физически обоснованными.

Остановимся на свойствах оператора Гильберта, обозначаемого обычно буквой Н. Это – линейный оператор, являющийся сверткой исходного сигнала и функции . Обратный оператор Н^–1 может быть найден путем решения уравнения  относительно s(t) переходом в частотную область с помощью преобразования Фурье. Учитывая правило преобразования Фурье для свертки, получим:

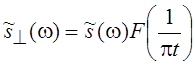, где .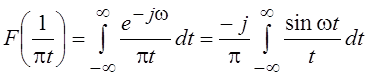

Интеграл 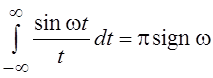, где 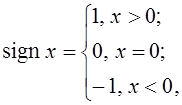– знаковая функция.

Таким образом, преобразование Фурье 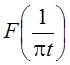, которое можно рассматривать как комплексный коэффициент передачи линейного фильтра, осуществляющего преобразование Гильберта, равно 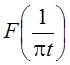=. Следовательно, .

Амплитудно-частотная характеристика такого фильтра 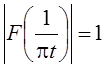, а фазо-частотная представляет собой 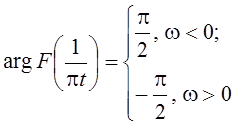. Используя данный результат, получим: 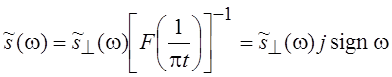, т. е., в отличие от прямого преобразования, изменился лишь знак. Следовательно, обратное преобразование Гильберта имеет вид:

.

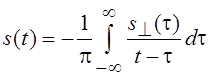С учетом частотного представления оператора Гильберта, , так как .

Оператор Гильберта унитарен, так как для его ядра 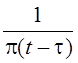 выполняется условие (5.4), что доказывается с помощью обобщенного равенства Парсеваля:

.

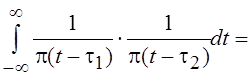
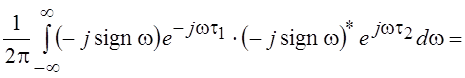
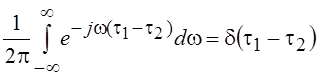Исходная функция s(t) и функция, преобразованная по Гильберту, ортогональны, что также доказывается с помощью обобщенного равенства Парсеваля:

,

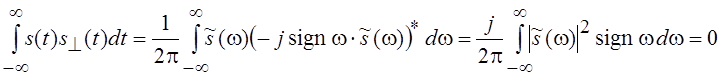как интеграл от нечетной функции в симметричных пределах.

Норма оператора Гильберта равна 1. Он не меняет энергии преобразуемых сигналов, т. е. .

Для узкополосных сигналов, для которых ширина спектра Dw много меньше центральной частоты w₀, гильбертову фазу F(t) целесообразно представить в виде F(t) = w₀t + g(t), а аналитический сигнал  записать как  = s(t) + js_^(t) = =.

Комплексная функция , определяющая законы амплитудной S(t) и угловой g(t) модуляции, называется комплексной огибающей. Зная комплексную огибающую, можно определить исходный сигнал s(t) = Re. Отметим, что комплексная огибающая является видеофункцией (центральная частота спектра равна нулю). Скорость ее изменения определяется шириной спектра исходного сигнала. Для иллюстрации вычислим спектр аналитического сигнала и комплексной огибающей для колокольного (гауссовского) импульса s(t) =, считая его узкополосным, т. е. 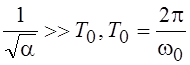 – период высокочастотного заполнения нашего сигнала.

В соответствии с теоремами о спектрах получим:

.

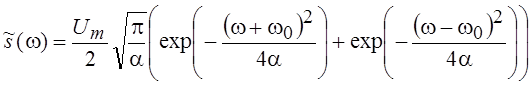Спектр аналитического сигнала равен F = Fs(t) + jFs_^(t). Как было показано выше, Fs_^(t) =  =, поэтому

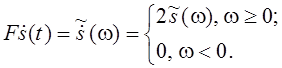
Для спектра комплексной огибающей, с учетом того, что  и теоремы о смещении спектра, выполняется соотношение: . Таким образом, для рассматриваемого сигнала окончательно получим:

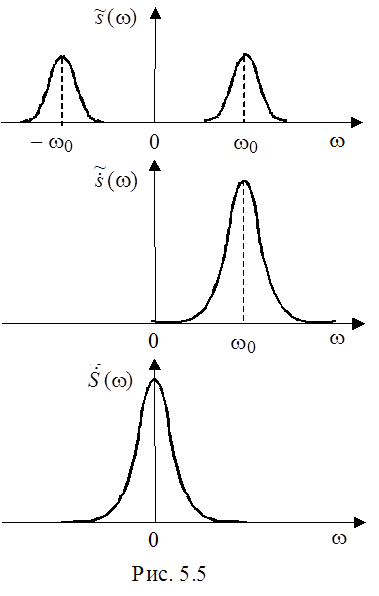
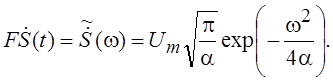
Рис. 5.5 иллюстрирует сказанное.

Комплексная огибающая упрощает решение задачи о преобразовании узкополосного сигнала  линейной системой с импульсной характеристикой , где S(t) и H(t) – огибающие сигнала и импульсной характеристики, а g(t) и b(t) – отклонение фазы от линейного закона.

С помощью интеграла Дюамеля комплексная огибающая выходного сигнала  находится как

=,

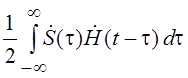где  и  – комплексные огибающие входного сигнала и импульсной характеристики фильтра. Выходной сигнал находится как

.

Контрольные вопросы

1.  Дайте определение оператора, функционала, функции.

2.  Как определяется понятие обратного оператора?