Линейные операторы и функционалы. Часть 3, страница 2

Сформулилруем следующую задачу.  При фиксированном значении энергии сигнала  и фиксированном одном из энергетических функционалов обеспечить экстремум другого. Это задача на условный экстремум. Функционал Лагранжа для нее имеет вид (фиксируем функционал E_q и условие нормировки):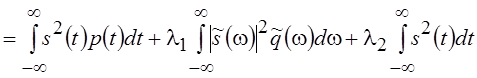. Для перехода к одной переменной t представим 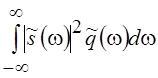 в виде скалярного произведения 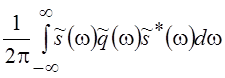 и воспользуемся обобщенным равенством Парсеваля 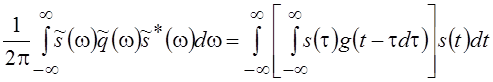. Выражение в квадратных скобках (свертка) соответствует временному образу произведения . Таким образом, необходимо исследовать на безусловный экстремум функционал

.

Как и в предыдущей задаче, с помощью представления функции s(t) в виде s(t) = s₀(t) + az(t), где s₀(t) – функция, для которой достигается экстремум, a – числовая переменная, z(t) – любая функция ÎL₂, приходим к необходимому условию экстремума 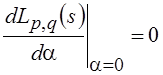. После дифференцирования, подстановки a =0  и элементарных преобразований получим  , где m₁ и m₂ – новые произвольные постоянные. Левую часть этого равенства можно записать в форме скалярного произведения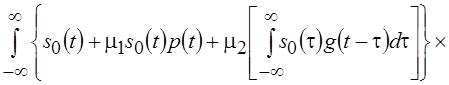

. Учитывая равенство нулю записанного скалярного произвдения при любой функции z(t), получим окончательное уравнение для определения s₀(t)

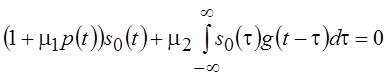                           (5.9)

В частотной области это уравнение примет вид (убедитесь в этом самостоятельно)  .

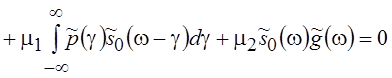Используем полученный результат для определения сигнала, у которого произведение временной протяженности на ширину спектра будет минимально. При этом временную протяженность Т_эфф определим как

,

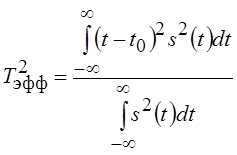а ширину спектра Dw_эфф как

,

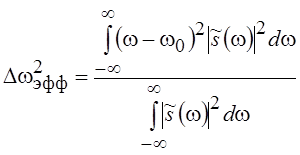где t₀ и w₀ – числа, характеризующие положение сигнала на оси t и спектра на оси w. Без потери общности они могут быть полжены равными нулю.

Кроме того, с учетом введенной выше нормировки 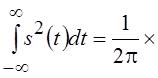 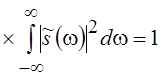. Ясно, что максимизация  Т_эфф·Dw_эфф или, что тоже самое,  эквивалентна минимизации одного из сомножителей при фиксированном значении другого. Таким образом , мы имеем предыдущую задачу с р(t) = t² и . Так как функции  во временной области соответствует g(t) = – d''(t), где d(t) – дельта-функция (проверьте это), то после подстановки g(t–t) в уравнение (5.9) и использования интегральных свойств производной дельта-функции, получим . Это линейное дифференциальное уравнение с переменными коэффициентами называется уравнением Эрмита (в квантовой механике его называют уравнением Шредингера).

Его решениями, собственными функциями дифференциального оператора Эрмита  являются Эрмитовы сигналы 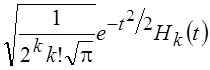. Глобальный минимум достигается при k = 0 и соответствует гауссовскому импульсу .

Таким образом, гауссовский (колокольный) импульс обеспечивает наилучшую концентрацию энергии на плоскости время-частота. Пр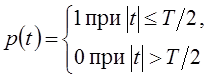и  и 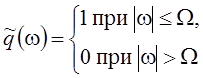 мы получим уже решенную задачу об импульсе, обеспечивающем максимальную концентрацию энергии в полосе частот [–W, W].

Оператор Гильберта.

Одним из основных понятий теории сигналов является комплексная функция , образованная из исходного вещественного сигнала s(t) добавлением мнимой составляющей s_^(t), которая определяется преобразованием Гильберта исходного сигнала 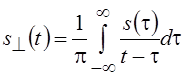. Эта комплексная функция называется аналитическим сигналом, т. е. .

Вещественная и мнимая части аналитического сигнала позволяют определить огибающую (модуль аналитического сигнала), характеризующую закон амплитудной модуляции и фазу (аргумент аналитического сигнала), определяющий закон угловой модуляции следующим образом:

– огибающая ,

– фаза .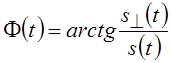

При этом аналитический сигнал  может быть записан в форме . Естественно, если мнимую часть аналитического сигнала определить не с помощью преобразования Гильберта, а иначе, то мы придем к другому определению огибающей, фазы и частоты, определяемой как производная от фазы, т. е. .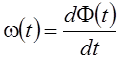

Таким образом, чтобы однозначно определить огибающую, фазу и частоту необходимо и достаточно указать правило построения мнимой части v(t) по исходному сигнала s(t), т. е. указать оператор А, осуществляющий преобразование v(t) = As(t).

При выборе оператора А необходимо потребовать, чтобы определенные на его основе понятия огибающей и фазы согласовывались бы с физическими инженерными представлениями. Вот эти представления.