Применение межотраслевого баланса в анализе стоимостных пропорций

6.5. Применение межотраслевого баланса в анализе стоимостных пропорций

Сравнительный анализ систем цен. Как отмечалось в 6.2, модель межотраслевых зависимостей цен (6.21) - (6.24) используется для расчетов и сравнительного анализа систем цен при разных способах начисления условно-чистой продукции (r_j = s_j+ v_j + m_j)- Рассмотрим некоторые характерные модификации общей модели ценообразования.

Формула "стоимости" (распределение прибавочного продукта пропорционально оплате труда). Пусть π₁ - единая по народному хозяйству норма прибавочного продукта (m_j= π₁v_j). Тогда

, jÎI      (6.43)

ш в векторно-матричном виде

P= PA + s + (1+ π₁)v,                                  (6.44)

где s, v — матрицы-строки коэффициентов амортизации и оплаты труда. Выражения (6.43), (6.44) могут быть упрощены, если амортизацию распределить по материально-вещественному составу (как затраты продукции машиностроения, строительства, животноводства) и добавить к соответствующим коэффициентам матрицы А. Получим матрицу . Вместо (6.43), (6.44) теперь имеем

, jÎI                      (6.45)

P= P + (1+ π₁)v               (6.46)

P= (1+ π₁)v (E - )^-1(6.47)

Выражение V= v(E- А)^-1 в (6.47) есть вектор коэффициентов полных затрат оплаты труда (народнохозяйственной зарплатоемкости продукции). Таким образом, цены прямо пропорциональны коэффициентам полных затрат оплаты труда (заработной платы). Коэффициент π₁ является общим множителем для всех цен и влияет только на абсолютный уровень цен, но не на их соотношения.

При использовании формул (6.43), (6.44) получаемые векторы цен ввиду малых значений коэффициентов s_j(в большинстве отраслей) почти пропорциональны полным затратам оплаты труда и мало зависят от значения π₁.

Цены по формулам (6.43 - (6.47) тесно связаны с трудоемкостью продукции. Если бы оплата труда была одинаковой во всех отраслях, то было бы v_j = kt, где k - оплата единицы затрат труда, и

, jÎI                                             (6.48)

, jÎI                                                       (6.49)

илиP= P  + (1+ π₁)kt

откуда P= (1+ π₁)kt (E - A)^-1                                (6.50)

                                                 P= (1+ π₁)kT

т.е. цены прямо пропорциональны полным трудовым затратам (с коэффициентом пропорциональности (1+ π₁k) а коэффициенты полных трудовых затрат на 1 руб. продукции отраслей равны. Поэтому дифференциация коэффициентов полных трудовых затрат, рассчитанных по данным межотраслевых балансов в ценностном выражении, свидетельствует об отклонениях фактических цен от цен, построенных по формулам (6.48) — (6.50). Например, по расчетам на основе усредненного межотраслевого баланса СССР коэффициенты полных трудовых затрат даже в разрезе 7 отраслей различаются в 1,9 раза.

Формула "усредненной стоимости" (прибавочный продукт пропорционален себестоимости продукции). Пусть π₂ — единый по народному хозяйству норматив прибавочного продукта на единицу себестоимости. Тогда

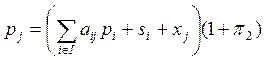           (6.51)

или

P= (1+ π₂) (PA+ s + v)              (6.52)

P= (1+ π₂) (s + v) [E – (1+ π₂ )A]^-1            (6.53)

Отсюда следует, что соотношение цен зависит от норматива прибавочного продукта π₂ (через коэффициенты матрицы ( [Е — (1 + π₂)A]^-1).

Формула цены производства (прибавочный продукт пропорционален сумме используемых производственных фондов). Отличительная особенность ценообразования по этой формуле состоит в том, что одновременно с исчислением цен требуется переоценивать производственные фонды и амортизационные отчисления.

Пусть d_ij — величина производственных фондов i-го вида (продукция машиностроения и строительства, скот), используемых в производстве единицы продукции j; эта величина есть сумма основных и оборотных фондов ( w_ij - норма амортизации i -го вида основных фондов, используемых в производстве единицы продукции j (доля годового износа); π₃ — единый по народному хозяйству норматив прибавочного продукта на единицу используемых производственных фондов. Общая сумма производственных фондов (в ценностном выражении) , используемых в производстве единицы продукции j, равна , а общая сумма амортизации — соответственно Система уравнений цен принимает вид ¹

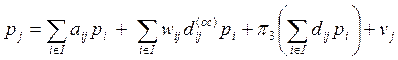 (6.54)

или

P=PA + PwD^(oc)+π₃PD+v;(6.55)

P=v (E – A - wD^(oc) - π₃ D)^-1              (6.56)