Моделирование поведения потребителей в условиях товарно-денежных отношений

5.2. Моделирование поведения потребителей в условиях товарно-денежных отношений

Основная часть потребительских благ распределяется между членами общества платным образом через торговлю и общественное питание. Поэтому для планового управления сферой потребления первостепенное значение имеет исследование закономерностей поведения потребителей на рынке. В основе построения моделей поведений потребителей лежит гипотеза, что потребители, осуществляя выбор товаров при установленных, ценах, имеющихся доходах и с учетом других обстоятельств, стремятся максимизировать уровень удовлетворения своих потребностей.

Анализ простой модели поведения потребителей. Пусть имеется и видов товаров. Исследуется поведение какой-либо группы или всей совокупности потребителей[1]. Спрос потребителей — это вектор Y = (y_f). При известных ценах на различные товары Р = (p_i) и величине дохода Dпотребители могут выбирать только такие комбинации товаров, которые удовлетворяют условию 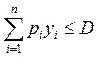(бюджетному ограничению). Предполагается, что предпочтения потребителей на множестве товаров выражаются целевой функцией u(Y).

Простая модель поведения потребителей имеет вид

u(Y)→max,

PY≤D,(5.6)

Y≥ 0.

Постулированный принцип оптимального поведения потребителей, разумеется, не следует понимать так, что потребитель перед тем, как купить какие-либо товары, проводит скрупулезные вычисления с помощью своей целевой функции на основе информации о полезных свойствах и ценах для всего множества товаров. Этот принцип отражает только генеральную тенденцию многочисленных актов потребительского выбора, а модель (5.6) - одно из возможных математических описаний такой тенденции.

Для учета в модели денежных сбережений населения можно использовать два подхода: считать денежные сбережения особым благом, имеющим полезность (его увеличение приводит к росту целевой функции) или же определять размер сбережений вне модели, рассматривая Dкак сумму расходов на приобретение товаров.

Геометрическая интерпретация модели для двух товаров представлена на рис. 5.4. Линия АВ соответствует бюджетному ограничению. Таким образом, выбор потребителей ограничен треугольником АОВ. Набор М (точка касания прямой АВ с наиболее отдаленной кривой безразличия) является оптимальным решением.

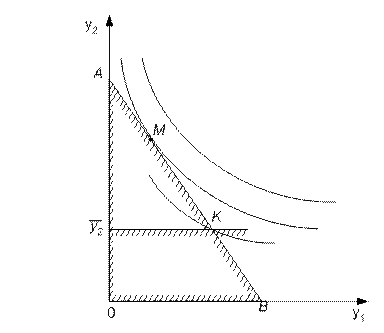
Рис. 5.4. Выбор потребителей при заданных ценах, доходе и дополнительных ограничениях

Выясним условия оптимальности решения для модели (5.6), опираясь на теорию нелинейного программирования.

Функция Лагранжа задачи (5.6) имеет вид

L(Y, λ) = u(Y) + λ (D - Р Y).

Множитель Лагранжа λ есть оптимальная оценка дохода. Частные производные 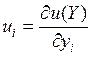 будем, как и в 5.1, интерпретировать как предельные полезные эффекты (предельные полезности) соответствующих потребительских благ.

Необходимыми условиями оптимума Y* (условиями Куна—Таккера) являются

(5.7)

При этом

                                                                                                  (5.8)

Если же  то соответствующий товар i не приобретается .

Очевидно, λ* > 0, что соответствует полному использованию дохода (PY* = D).

Равенство (5.8) можно записать так:

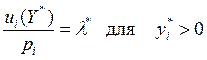                        (5.9)

или же

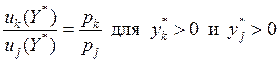                                 (5.10)

Это означает, что потребители должны выбирать товары таким образом, чтобы отношение предельной полезности к цене товара было одинаковым для всех товаров. Или, что равносильно, предельные полезности выбираемых товаров должны быть пропорциональны ценам.

Направления использования модели. Основными направлениями использования модели являются: изучение зависимостей покупательского спроса от цен и доходов, построение ЦФП, регулирование цен и доходов для достижения сбалансированности спроса и товарного предложения.

Целевая функция потребления не может наблюдаться непосредственно. Но она может быть выявлена при анализе поведения потребителей, если это поведение достаточно хорошо описывается моделью (5.6).

Методика "восстановления" целевой функции потребления включает несколько этапов.

Сначала выбирается одна или несколько математических моделей (формул) целевой функции, удовлетворяющих некоторым теоретическим гипотезам (например, квадратичная или логарифмическая функция).

Из анализа модели (5.6) известно, что для разнообразных товаров, приобретаемых при различных ценах и доходах, теоретически должны выполняться условия (5.8). Поэтому каждому сочетанию s наблюдаемых величин покупок и цен соответствует п уравнений , где  - погрешность. Далее ставится стандартная задача математической статистики: оценка параметров системы регрессионных у равнений. При этом требуется, чтобы число уравнений существенно превышало число неизвестных параметров. В заключение проводится сравнение первоначально выбранных математических моделей и, в конечном счете, принимается та из них, которая наилучшим образом аппроксимирует статистические наблюдения.