Модели с лагами капитальных вложений. Во всех анализировавшихся выше моделях допускалось отсутствие лага между производственным накоплением и приростом национального дохода. Это — серьезное упрощение реальности. Как отмечалось, инвестиционные лаги являются важными характеристиками процесса воспроизводства.
Модель
с сосредоточенным лагом. Обозначим величину сосредоточенного лага ![]() . Тогда
. Тогда 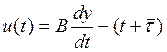 , а
общая модель воспроизводства национального дохода приобретает вид
, а
общая модель воспроизводства национального дохода приобретает вид
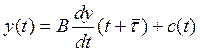 (10.12)
(10.12)
При постоянной норме производственного накопления а0 получаем следующее обобщение модели
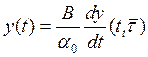 (10.13)
(10.13)
Модель
(10.13) представляет собой дифференциальное уравнение с запаздывающим
аргументом (или дифференциально-разностное уравнение). Исследование этого уравнения
(см. ДМНХ, с. 56) дает формулу для определения темпа прироста национального дохода ![]() , равного темпу прироста потребления:
, равного темпу прироста потребления:
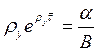 (10.14)
(10.14)
Из
анализа (10.14) следует, что ![]() монотонно убывает при
увеличении
монотонно убывает при
увеличении ![]() . Уменьшение темпа национального
дохода при постоянном, а тем более увеличивающемся
лаге объясняется тем, что все возрастающая величина накопления "замораживается"
и не может использоваться для расширения
производства. Увеличение доли накопления
. Уменьшение темпа национального
дохода при постоянном, а тем более увеличивающемся
лаге объясняется тем, что все возрастающая величина накопления "замораживается"
и не может использоваться для расширения
производства. Увеличение доли накопления ![]() хотя
и поднимает темп национального
дохода, но уже медленнее пропорционального
увеличения. В табл. 10.1 приводятся значения
хотя
и поднимает темп национального
дохода, но уже медленнее пропорционального
увеличения. В табл. 10.1 приводятся значения ![]() при
В = 3,5 и трех значениях а0.
при
В = 3,5 и трех значениях а0.
|
|
|
||
|
|
|
|
|
|
0 |
0,286 |
0,057 |
0,029 |
|
1 |
0,226 |
0,054 |
0,028 |
|
2 |
0,194 |
0,052 |
0,027 |
|
3 |
0,171 |
0,049 |
0,026 |
|
4 |
0,154 |
0,047 |
0,025 |
Анализ модели (10.12) с заданной траекторией потребления с(t) = с(0)ertвыявляет свойства, аналогичные свойствам модели без лага, но при более низких темпах национального дохода (см. ДМНХ, с. 57).
Модель с распределенным лагом. Производственное накопление с распределенным лагом определяется по формуле
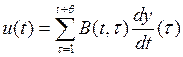 ,
,
где B(t, ![]() ) — затраты капитальных вложений в момент t, необходимые для получения единицы прироста
национального дохода в момент
) — затраты капитальных вложений в момент t, необходимые для получения единицы прироста
национального дохода в момент ![]() . При этом затраты капитальных вложений "распределяются" внутри
периода протяженностью
. При этом затраты капитальных вложений "распределяются" внутри
периода протяженностью ![]() лет. Общая капиталоемкость в момент
tсоставляет
лет. Общая капиталоемкость в момент
tсоставляет
![]()
Континуальный аналог формулы и(t) имеет вид
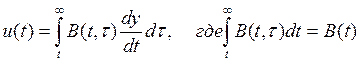 .
.
Будем
предполагать, что ![]() - убывающая функция от
- убывающая функция от ![]() . Этому предположению соответствует,
в частности, функция
. Этому предположению соответствует,
в частности, функция
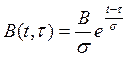 ,
,
в которой параметр ![]() характеризует степень распределенности
лага (чем больше
характеризует степень распределенности
лага (чем больше ![]() , тем более растянут лаг).
Например, при s = 2 имеем
, тем более растянут лаг).
Например, при s = 2 имеем
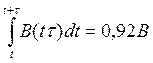 ,
,
при s = 4
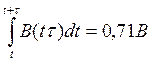
При постоянной норме накопления и(t) = аоу(t), и поэтому
![]()
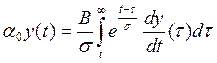
Преобразования этого уравнения приводят в конечном счете к решению:
![]() (10.15)
(10.15)
Таким образом, учет распределенного лага при развитии
с постоянной нормой накопления приводит к уменьшению постоянного темпа прироста
национального дохода от ![]() до
до 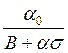 .
.
[1] В отличие от коэффициентов статического межотраслевого баланса (затраты i-й продукции на производство единицы j-й продукции) коэффициент а включает не только текущие производственные затраты, но и затраты на возмещение выбытия и капитальный ремонт основных производственных фондов.
[2] В общем случае акселератор - это коэффициент пропорциональности между выходной величиной и скоростью изменения входной величины.
[3] Исходное соотношение имеет вид: .
Но поскольку: , то .
[4]В частности, при имеем
При этом, если , то рост национального дохода затухает и имеет предел
Подробнее о влиянии динамики коэффициента В на технологический прирост см. в ДМНХ, с. 49.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.