Ниже анализируется ряд модификаций модели воспроизводства национального дохода, построенных на основе (10.4).
Простейшая модель. Наиболее простая модель воспроизводства национального дохода формулируется при использовании двух допущений: а) пропорциональности производственного накопления прироста национального дохода в тот же момент времени; б) независимости (экзогенности) динамики потребления:
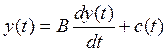 (10.5)
(10.5)
Таким образом, простейшая модель воспроизводства национального дохода выражается линейным неоднородным дифференциальным уравнением первого порядка.
Коэффициент В — капиталоемкость национального дохода (отношение производственного накопления к приросту национального дохода) ; этот коэффициент называют также акселератором[2].B=bA, где B— капиталоемкость валового общественного продукта[3]. В последующих числовых иллюстрациях принимается а = 0,6, b — 1,4, откуда В = = 3,5.
В соответствии с (10.5) при заданном параметре В динамика национального дохода определяется траекторией c(t). Проанализируем поведение решения при разных гипотезах о динамике потребления.
1. с (t) = 0. Гипотеза, что весь национальный доход направляется на расширение производства и потребление отсутствует, разумеется, нереалистична. Но она позволяет оценить максимально возможный темп увеличения национального дохода, ограниченный только материалоемкостью и капиталоемкостью производства. При с(t) = 0 в соответствии с теорией дифференциальных уравнений имеем
![]() (10.6)
(10.6)
Величину
![]() — будем называть технологическим темпом прироста.
— будем называть технологическим темпом прироста.
Приняв
В = 3,5, получаем ![]() — 0,286; это
соответствует постоянному ежегодному приросту
на 33,1 %. При таком темпе удвоение национального дохода достигается за 2,4 года, утроение - за 3,8 года.
— 0,286; это
соответствует постоянному ежегодному приросту
на 33,1 %. При таком темпе удвоение национального дохода достигается за 2,4 года, утроение - за 3,8 года.
Рассматривая значение коэффициента капиталоемкости национального дохода как функцию времени В = B(t), получаем
![]()
где
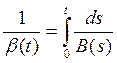
С возрастанием B(t) технологический темп убывает, а с уменьшением B(t) - увеличивается[4].
2. c(t) = с(0) = const. Общее решение уравнения (10.5) представим в виде
![]()
При t= 0 имеем ![]() или
или ![]() .
.
Отсюда
![]() (10.7)
(10.7)
Очевидно, у(t) > 0, если y(0)> с(0), т.е. в начальный момент потребляется не весь национальный доход. Тогда в соответствии с (10.7) национальный доход растет возрастающим темпом, поскольку в объеме y(t) непрерывно увеличивается "вес" слагаемого
![]()
В начале
периода (при t= 0) темп прироста ![]() составляет
составляет
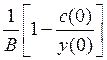 .
.
В пределе (при t® ¥ ) он
увеличивается до![]() .
.
Например, если y(0) = 600 млрд. руб., с(0) = 480 млрд. руб., В = 3,5, то за первый год прирост составит 6,62%, за пятый - 14,57, за десятый - 25,37%. За 10 лет при таких темпах национальный доход увеличился бы в 4,92 раза, а доля потребления уменьшилась бы с 0,8 до 0,186.
3.![]() . Это означает, что
потребление увеличивается с непрерывным темпом прироста г. Общее решение имеет
вид
. Это означает, что
потребление увеличивается с непрерывным темпом прироста г. Общее решение имеет
вид

Из него при t = 0 находим
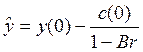 .
.
Таким образом,
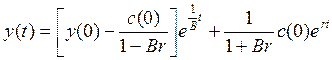 (10.8)
(10.8)
Экономически приемлемые траектории изменения
национального дохода получаются только в том случае, когда заданный темп
прироста потребления меньше технологического темпа прироста национального дохода:
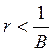 . В противном случае (при
. В противном случае (при 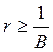 ) доля накоплений быстро
падает, а вместе с ней уменьшается и темп прироста национального дохода. Далее, в некоторой точке
) доля накоплений быстро
падает, а вместе с ней уменьшается и темп прироста национального дохода. Далее, в некоторой точке ![]() темп становится равным нулю, а в точке
темп становится равным нулю, а в точке ![]() объем
национального дохода становится равным нулю (подробнее см. в ДМНХ, с. 50 — 51). Поэтому принимаем
объем
национального дохода становится равным нулю (подробнее см. в ДМНХ, с. 50 — 51). Поэтому принимаем 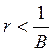 , откуда
, откуда ![]() .
.
Траектория изменения национального дохода в этом случае зависит от знака коэффициента первого слагаемого в (10.8). Преобразуем этот коэффициент следующим образом:
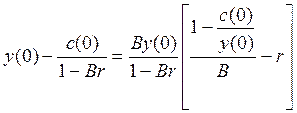
Обозначим
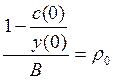 .
.
Величина
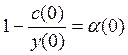
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.