Модели динамики общественного продукта и национального дохода, страница 3

есть норма производственного накопления в начальный момент времени. Отсюда р₀ равен произведению этой нормы на технологический темп прироста, или отношению нормы производственного накопления в начальный момент времени к капиталоемкости прироста национального дохода:

.

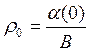Подставив р₀ в (10.8), получим

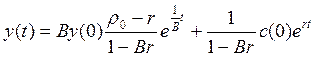               (10.9)

Из (10.9) следует, что поведение решения во многом зависит от соотношений между rи р₀.

Рост с постоянной и монотонно изменяющейся нормой накопления. Проанализируем три типа экономического развития, различающиеся темпами прироста потребления и динамикой нормы накопления: 1) r = р₀; 2) r>р₀; 3) r<р₀.

Постоянная норма накопления. При r = р₀ первое слагаемое в (10.9) обращается в нуль. Темп прироста национального дохода равен темпу прироста потребления:

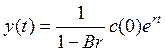               (10.10)

Экономическое развитие осуществляется с постоянной нормой накопления . Поскольку 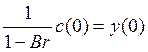 и 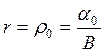, то эквивалентным является решение в более простом виде:

                       (10.11)

В соответствии с (10.11) при постоянной норме производственного накопления темп прироста национального дохода пропорционален норме накопления и обратно пропорционален капиталоемкости прироста национального дохода. При а₀ = 0,20 имеем  = 0,057.

В современной экономико-математической литературе модель (10.11) более известна как модель Харрода-Домара. Однако впервые она была сформулирована советским экономистом Г.А.Фельдманом в конце 20-х гг. (что признается западными экономистами-математиками) и использовалась при разработке первого генерального плана развития народного хозяйства СССР (см. ДМНХ, с. 52).

Следует подчеркнуть, что в модели (10.11) норма производственного накопления не может интерпретироваться как регулируемый параметр (экзогенная переменная). Если принимается , то динамика национального дохода описывается более сложным образом, чем по формуле (10.11). Этот случай анализируется в 10.2.

Уменьшающаяся норма накопления. При r> первое слагаемое решения (10.9) отрицательно, второе положительно. При этом первое слагаемое по абсолютной величине растет быстрее второго. Вследствие этого темп прироста национального дохода падает, норма накопления уменьшается до нуля, а затем становится отрицательной. Поведение решения качественно аналогично рассматривавшемуся выше случаю 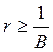. Здесь также можно установить моменты достижения нулевого темпа (t₁) и нулевого объема национального дохода (t₂)- Например, при r = 0,08 имеем t₁= 4,98, t₂ = 11,16.

Увеличивающаяся норма накопления. При r< оба слагаемых в решении (10.9) положительны, при этом первое слагаемое растет быстрее второго. Поэтому темп прироста национального дохода непрерывно увеличивается от  в начальный момент до в пределе. Норма накопления также непрерывно увеличивается.

Рассмотренные три варианта динамики и структуры национального дохода, различающиеся соотношениями темпов rи , изображены на рис. 10.1. Заметим, что варианту 2 качественно соответствует поведение решения (10.8) при 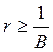, а варианту 3 - поведение решений (10.6), (10.7).

Рис. 10.1. Динамика национального дохода (а) и производственного накопления (б) при экспоненциальном росте потребления: 1), 2) ,3) .

На неограниченном интервале времени при постоянной капиталоемкости "интересы" потребления и накопления уравновешиваются при . Если , то реальный выигрыш в объеме потребления достигается только на отрезке [0, t₁]. Если же, то темп национального дохода возрастает только за счет опережающего роста накопления. Очевидно, что и такой тип экономического развития ("накопление ради накопления") может быть целесообразным только на ограниченном интервале времени. Таким образом, анализ модели обнаруживает существенные недостатки траекторий развития при условии монотонно понижающейся или монотонно повышающейся нормы накопления в течение длительного времени.