Многоцелевая (векторная) оптимизация

2.5. Многоцелевая (векторная) оптимизация

Построение глобального критерия оптимальности (или скалярной целевой функции) не является необходимым условием поиска оптимальных народнохозяйственных решений. Более общей моделью народного хозяйства является модель векторной оптимизации, или оптимизационная модель с векторной целевой функцией.

Векторная целевая функция включает такие частич­ные целевые функции , которые не сводятся (по крайней мере, на первом этапе моделирования) в единую целевую функцию и выражают степени удовлетворения различных потребностей общества: повышение материального благосостояния, удовлетворение социальных запросов членов общества, упрочение и развитие систем общественных отношений, обеспечение безопасности развития и т.п. Благодаря этому обходятся трудности непосредственного сопоставления наиболее разнокачественных целей.

Будем исходить из того, что рост каждой частичной целевой функции соответствует увеличению степени удовлетворения определенных групп потребностей. Очевидно, общий уровень удовлетворения потребностей безусловно возрастает, когда значение хотя бы одной целевой функции возрастает, а значения остальных не убывают.

Решение, оптимальное по одной из частичных целевых функций, называется субоптимальным. В общем случае субоптимальные решения для разных частичных целевых функций не совпадают. Отсюда вытекает необходимость выбора таких решений, которые являются наилучшими с точки зрения совокупности частичных целевых функций.

Эффективные решения (оптимум по Парето). Вариант будем называть эффективным, если не существует какого-либо другого варианта X, для которого значения всех функций fⁱ(X) не меньше , а значение хотя бы одной функции строго больше[1]. Иначе говоря, не существует такого X, что .

Множество эффективных вариантов обозначим . Такое множество называют множеством Парето, а элемент этого множества  — оптимумом по Парето (по имени известного итальянского экономиста-математика конца XIX — начала XX вв.).

Любое из решений  не может быть улучшено ни по одной частичной целевой функции fⁱ(X) без ухудшения по какой-либо другой из них. Например, если из множества возьмем два таких варианта X_Aи X_B, что fⁱ₁(X_A)> fⁱ₁(X_B),  то обязательно найдется какая-нибудь i-я функция, по которой fⁱ₂(X_A)> fⁱ₂(X_B).

Первый логический этап векторной оптимизации — нахождение множества. При этом основное внимание можно сосредоточить на исследовании множества эффективных значений функции.

Решить указанную задачу в полном виде, как правило, трудно. Ситуация облегчается, если множество  замкнуто и выпукло, а максимизируемые функции fⁱ(X)  — вогнутые (т.е. задачи субоптимизации есть задачи выпуклого программирования).

При выполнении указанных условий справедливы следующие утверждения:

1) для любого X  существует такой полуположительный вектор L=(l_i) с компонентами, удовлетворяющими равенству

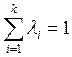, что  достигается для  X=.

2) если задан векторL=(l_i)>0, где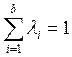, то задача  дает эффективные варианты (один или несколько) X .

Иначе говоря, любое решение задачи векторной оптимизации является решением задачи скалярной оптимизации с целевой функцией, которая представляет собой взвешенную (или средневзвешенную) сумму частичных целевых функций. Второе утверждение указывает конструктивный метод определения эффективных вариантов: необходимо решать задачу скалярной оптимизации с целевой функцией F_s(X), рассматривая l_i как меняющиеся параметры, на которые наложены условия l_i>0 и 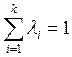. В случаях когда L- орт (имеет только одну положительную компоненту, равную единице), получаем субоптимальные решения.

Если множество невыпукло и не все fⁱ(X) вогнутые, то нахождение эффективных вариантов усложняется. Применяются разнообразные приемы зондирования Парето-границы и нахождения ее характерных точек (в частности, вершин многогранника).

Определение множества эффективных решений сужает область выбора наилучших решений. Следующий этап выбора решений представляет собой поиск компромисса между несовпадающими и противоречивыми целями. Требуется определять принципиальную схему разумного компромисса, которая позволила бы выделить в некотором смысле наилучшее решение или минимальное множество, внутри которого решения неразличимы по своей предпочтительности. Наиболее распространены две схемы компромисса между частичными целевыми функциями: условная субоптимизация и скаляризация векторного критерия оптимизации.