Многоцелевая (векторная) оптимизация, страница 3

Степень достижения «идеального» состояния по каждой частичной целевой функции определяется как 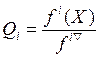. Общая скаляризованная целевая функция имеет вид

F₄(X) = ,.                     (2.13)

Определение max  можно интерпретировать как «подтягивание» наиболее «отстающего» из критериев (степени удовлетворения какой-то группы потребностей) до уровня других критериев (степени удовлетворения других групп потребностей). Поскольку в функции (2.13) сопоставляются только относительные величины, трудности соизмерения различных целевых функций обходятся. Этим во многом объясняется широкое использование принципа максимина в прикладных оптимизационных моделях (см. гл. 8,11—13)

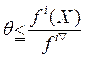Обозначим =θ. Отсюда следует, что  или же , i= 1,..., k. Поэтому задача нахождения max  может быть представлена в виде максимизации числа θ с дополнительными ограничениями по частичным целевым функциям:

θ →max,

(2.14)

Рассмотренные приемы скаляризации векторного критерия оптимальности показывают, что между моделями скалярной и векторной оптимизации нет жестких границ. Векторная оптимизация не есть только отрицание оптимального планирования с глобальным (скалярным) критерием оптимальности. Использование методов скаляризации векторного критерия снова приводит нас к оптимизационной модели с единым критерием (т.е. здесь происходит «отрицание отрицания»). Но возвращение к модели с единым критерием оптимальности осуществляется на качественно новой основе.

Бели в ранее анализировавшихся моделях народного хозяйства принципы сочетания разнокачественных целей постулировались и глобальный критерий вводился априорно, то в моделях векторной оптимизации единый критерий в определенном смысле генерируется. Выбору единого критерия оптимальности предшествует исследование множества эффективных вариантов и обсуждение возможных схем компромисса между частичными критериями.

В то же время необходимо подчеркнуть, что модель векторной оптимизации предоставляет больше возможностей для участия исследователя в процессе поиска лучших решений.

Квазиоптимизация. Суть задачи квазиоптимизации состоит в том, что находится не оптимальное решение, а некоторое множество решений, близких к оптимальному. Такое множество  называется квазиоптимальным множеством.

Рассмотрим типичную постановку квазиоптимизационной задачи. Необходимо найти множество вариантов из XÎ, для которых значение максимизируемой целевой функции f(X) уступает максимальному значению этой функции не более заданной величины Δf:

=XÇ[X:f(X)-Δf        (2.15)

Большой интерес представляет соединение принципов квазиоптимизации и векторной оптимизации.

Задачу квазиоптимизации можно трактовать как определение множества решений, вполне удовлетворительных с точки зрения главного критерия оптимальности. Тогда на множестве можно выбирать решения, удовлетворяющие требованиям других, менее важных критериев оптимальности, например . Действительно, если скалярный

критерий f¹(X)не учитывает всего многообразия целей развития народного хозяйства, то, вероятно, можно ценой некоторого отступления от максимума f¹(X)попытаться учесть требования других критериев.

Учет всей совокупности критериев оптимальности, упорядоченных по степени важности (приоритету), возможен при использовании метода последовательной квазиоптимизации.

Пусть все критерии оптимальности (частичные целевые функции) пронумерованы в соответствии со своей важностью: f¹(X), f²(X), f³(X)…. Последовательная квазиоптимизация представляет собой многоэтапный процесс решения квазиоптимизационных задач на последовательно сужающемся множестве допустимых вариантов. На первом этапе определяется квазиоптимальное множество

На втором этапе — квазиоптимальное множество

и т.д.[2] На этапах последовательной квазиоптимизации можно применять все рассматривавшиеся выше методы векторной оптимизации.