15.5. Методы аппроксимации производственных возможностей
Другой подход к согласованию решений в системе моделей, основанный на агрегировании информации при ее движении с нижних уровней системы и детализации в обратном направлении, связан с аппроксимацией множества производственных возможностей. Центральной идеей этого подхода является передача вышестоящему уровню информации о возможностях подсистем в относительно узкой области — окрестности предполагаемого оптимума. Комбинирование различных способов аппроксимации производственных возможностей объектов разного уровня позволяет построить систему моделей многоступенчатой оптимизации, последовательно реализующую принцип обратимого сжатия экономической информации [16][1].
Производственные возможности любого хозяйственного объекта (предприятия, отрасли, народного хозяйства в целом) могут приближенно описываться двумя способами: построением выпуклого многогранника и заданием аппроксимирующей гиперплоскости.
При аппроксимации с помощью выпуклого многогранника объект может быть представлен в виде:
![]() ,
, ![]() (15.27)
(15.27)
Здесь z — вектор продукции (положительные компоненты) и затрат
(отрицательные компоненты) ; al— опорные планы
развития и функционирования объекта, выбранные некоторым способом в аппроксимируемой области;![]() — интенсивность использования l-го опорного плана.
— интенсивность использования l-го опорного плана.
Эквивалентная матричная запись условий (15.27) имеет вид:
![]() ,
, ![]() (15.28)
(15.28)
где А — матрица опорных планов, x — вектор интенсивностей их использования (внутренних переменных хозяйственного объекта), е — вектор, все компоненты которого равны единице.
Совместное функционирование объектов описывается вектором ![]() , где каждый zk задается условием
(15.27) или (15.28).
, где каждый zk задается условием
(15.27) или (15.28).
Варианты функционирования объекта определяются критерием оптимальности f(z) и внешними условиями, задающими его взаимосвязи с другими объектами экономической системы (ресурсные ограничения и т.д.). В общем виде эти условия можно записать как z ³ b. Положительные компоненты вектора z отражают задания объекту по выпуску конечной продукции, отрицательные - выделенные ему ресурсы; нулевые компоненты относятся к условиям, описывающим производство и использование промежуточной продукции.
Сделанные предположения позволяют сформулировать модель объекта, включающую аппроксимацию его производственных возможностей:
f(z)—> max;
z ³ b(15.29)
![]() ,
, ![]()
Варьируя параметры модели (15.29), можно получить совокупность локально-оптимальных планов zsи на их основе уточнить аппроксимацию производственных возможностей (15.27) в окрестности предполагаемого оптимума
![]() ,
, ![]() (15.30)
(15.30)
заменяя условиями (15.30) соотношения (15.26). Будем далее предполагать, что аппроксимация (15.27) описывает производственные возможности в окрестности оптимального варианта его развития.
Второй способ аппроксимации — построение в окрестности ожидаемого оптимума одного уравнения (аппроксимирующей гиперплоскости) с точным равенством для оптимального плана задачи (15.29).
Основные этапы построения такой гиперплоскости состоят в следующем. Пусть z° - оптимальный план
объекта (задачи (15.29)), v° -оптимальные оценки внешних условий (z ³ b). Если вектор z= z° + Dz (при малых Dz) допустим в задаче
(15.29) , то очевидно Df = f(z) - f(z°) £ 0. Рассматривая же Dz как параметр задачи
(15.29), изменение ее критерия можно оценить как Df = v°Dz, откуда v° (z - z°) £ 0, и, переходя к
нормированным оценкам 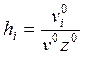 , имеем в окрестности z° уравнение
гиперплоскости
, имеем в окрестности z° уравнение
гиперплоскости
hz £ 1 (15.31)
Очевидно, что для оптимального плана z° условие (15.31) выполняется как равенство.
Аппроксимация (15.31) показывает, что в окрестности оптимального плана допустимы изменения структуры выпускаемой продукции (или ресурсов), но только такие, при которых сохраняется неравенство hz £ 1, т.е. при которых замена одних видов продукции другими производится в соответствии с коэффициентами производственной взаимозаменяемости h.
Использование аппроксимации (15.31) позволяет перейти к агрегированному описанию объекта введением обобщенного продукта Z = = hzи одним линейным ограничением z£ 1.
Распространяя процедуру агрегирования на параметры внешних условий b, В = hb, можно сформулировать исходную задачу развития объекта в агрегированных показателях:
![]()
B£ Z£ 1. (15.32)
Здесь ![]() — критерий оптимальности модели объекта
(15.29), переформулированный в агрегированных показателях. В задаче (15.32) отсутствует информация о
возможных изменениях структуры агрегированных показателей. Поэтому операторы
дезагрегирования двойственных оптимальных решений
— критерий оптимальности модели объекта
(15.29), переформулированный в агрегированных показателях. В задаче (15.32) отсутствует информация о
возможных изменениях структуры агрегированных показателей. Поэтому операторы
дезагрегирования двойственных оптимальных решений ![]() задачи
(15.32) определяются в предположении сохранения прежней структуры выпуска и
оптимальных цен:
задачи
(15.32) определяются в предположении сохранения прежней структуры выпуска и
оптимальных цен:
![]() (15.33)
(15.33)
Основное свойство введенных процедур дезагрегирования состоит в том, что
детализированные планы ![]() , определенные в
соответствии с (15.33), сохраняют уровень стоимостной оценки агрегированного решения
, определенные в
соответствии с (15.33), сохраняют уровень стоимостной оценки агрегированного решения ![]() :
:
![]()
Наиболее последовательно методы аппроксимации производственных возможностей используются в системе моделей многоступенчатой оптимизации, отражающей основные черты оптимального планирования производственно-технологической структуры экономики. Построенная на этих идеях экспериментальная многоступенчатая народнохозяйственная модель объединяет три уровня производственной иерархии: предприятие — отрасль — народное хозяйство. Модель имеет следующий вид:
и(х)—► max;
![]() ;
;
![]() (15.34)
(15.34)
![]()
![]()
![]()
Здесь
и(x) — народнохозяйственный критерий
оптимальности; Аkl — матрица опорных планов l-го предприятия
k-й отрасли; хkl— допустимый план предприятия, рассматриваемый
как комбинация опорных планов; ![]() план k-й отрасли, составленный в
детализированной номенклатуре:
план k-й отрасли, составленный в
детализированной номенклатуре:
![]() — народнохозяйственный план в
детализированной номенклатуре.
— народнохозяйственный план в
детализированной номенклатуре.
Вектор х распадается на вектор конечного продукта (с неотрицательными компонентами) и вектор суммарных затрат лимитированных ресурсов (с неположительными компонентами), включающий в данной постановке как народнохозяйственные, так и отраслевые ресурсы. Вектор Ъ включает ограничения по лимитированным ресурсам, фиксированным элементам конечного продукта (запасы, сальдо экспорта-импорта).
Использование этой модели как основы трехступенчатой оптимизации народного хозяйства рассматривается в ВСМ, с. 90 — 93.
[1] Этот подход разрабатывался в ЦЭМИ АН ССОР под руководством В.Ф.Пугачева.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.