Динамические модели с двусторонними связями отрезков планового периода

13.5. Динамические модели с двусторонними связями отрезков планового периода

В данном разделе анализируются Прикладные межотраслевые модели, которые в соответствии с классификацией в 13.1 могут быть отнесены к типу "полностью динамических". Принципиальным преимуществом моделей этого типа по сравнению с рекурсивными и квазидинамическими является более адекватное отражение причинно-следственных зависимостей между прошлым, настоящим и будущим развитием народного хозяйства. Особенность "полностью динамических" моделей с вычислительной точки зрения заключается в том, что показатели, относящиеся к различным временным отрезкам (годам, подпериодам) планового периода, определяются посредством решения единой "межвременной" задачи. Соответственно возрастают требования к математическому и техническому обеспечению проводимых расчетов.

Среди моделей, отвечающих формальным признакам "полностью динамических", целесообразно различать модели со "слабой" и "сильной" экономической взаимосвязанностью временных отрезков. Примерами моделей со "слабой" экономической взаимосвязанностью являются обобщения оптимизационных рекурсивных моделей, в которых взаимосвязанность временных отрезков достигается благодаря включению интегральной целевой функции. "Сильная" экономическая взаимосвязанность временных отрезков достигается благодаря достаточно полному отражению в модели долговременных инвестиционных процессов с помощью сквозных динамических производственных способов, лаговых соотношений распределения капитальных вложений, воспроизводства основных фондов, производственных мощностей и потребительского имущества.

Ниже рассматриваются две модели с временными взаимозависимостями. Первая (с распределенными лагами) в полной мере относится к динамическим моделям с "сильной" взаимосвязанностью. Вторая занимает в этом смысле промежуточное положение, обладая важными свойствами полностью динамических моделей и сохраняя преимущества моделей рекурсивного типа.

Модель с распределенными лагами. Межотраслевая балансовая модель с распределенными инвестиционными лагами предложена Э.Ф. Барановым ([6. С. 273 — 284]). Она включает уравнения балансов производства и распределения продукции и балансы основных фондов и представляет собой систему из 2nТ линейных уравнений (где п — число отраслей). Позднее балансовая модель была преобразована И.С. Матлиным в оптимизационную путем замены равенств неравенствами (по балансам фондов), введения ограничений по трудовым ресурсам, условий формирования фонда потребления и критерия оптимальности ([2. С. 60-65]; [9. С. 168 - 184]).

Ключевыми элементами модели являются зависимости между капитальными вложениями, вводом и выбытием основных производственных фондов и объемами производства. Ниже приводится модификация модели, включенная в комплекс укрупненных межотраслевых моделей, разработанный ГВЦ Госплана СССР и ЦЭМИ АН СССР. В запись модели внесены изменения унифицирующего характера.

1. Балансы производства и распределения продукции:

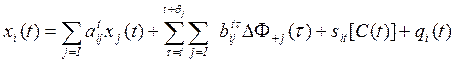               (13.34)

 .

Зависимость, определяющая потребности в капитальных вложениях на расширенное воспроизводство для , в точности соответствует (12.4); s_it — функция, преобразующая вектор целевых показателей в конечную продукцию 1-й отрасли.

2.         Балансы основных производственных фондов по отраслям-потребителям:

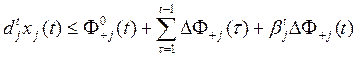           j Î I, (13.35)

Здесь используются упрощенные по сравнению с (12.7), (12.9), (12.13) зависимости. Отметим, что вплоть до года объемы действующих производственных фондов предопределены капитальными вложениями допланового периода.

3.  Балансы трудовых ресурсов:

           (13.36)

где s_lt — функция, характеризующая потребности в трудовых ресурсах для непроизводственной сферы в зависимости от вектора достигаемых целевых показателей.

4.        Критерий оптимальности. Максимизируется функция, определяемая на векторе целевых показателей за весь плановый период, в частности:

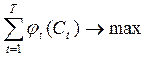(13.37)

Кроме обязательных условий (13.34) — (13.37) (их число равно 2nТ, что при стандартной 18-отраслевой классификации и плановом горизонте в 15 лет дает 540 уравнений и неравенств), модель включает ограничения для отдельных лет планового периода (по объемам производства некоторых отраслей, фонду капитальных вложений, использованию отдельных ресурсов) и для пятилеток (по фонду капитальных вложений), а также условия неотрицательности переменных x_j(t) и . Рассматриваемая модель имеет относительно узкие возможности оптимизации. С точки зрения методологии оптимизационного подхода наиболее искусственным является априорное жесткое установление распределенных инвестиционных лагов по всем отраслям.