Динамические модели с двусторонними связями отрезков планового периода, страница 2

Оптимизационная многопериодная модель. Многопериодные модели совмещают ряд преимуществ рекурсивных и полностью динамических моделей. В них расчеты ведутся на последние годы пятилетий, связываемых в рамках долгосрочного периода. Рассматриваемая ниже модель разработана в НИЭИ при Госплане СССР, предназначена для обоснований темпов, пропорций, отраслевой структуры экономики на долгосрочный период.

Модель построена в разрезе укрупненных отраслей промышленности и народного хозяйства. Ее принципиальной особенностью является учет взаимозаменяемости основных производственных фондов и трудовых ресурсов. Распределение капитальных вложений между отраслями осуществляется не только для увеличения производства, но и с целью регулирования роста производительности труда через рост его фондовооруженности.

Ниже дается описание модели без блока внешней торговли и с незначительными" упрощениями.

1. Балансы производства и распределения продукции:

      i Î I, t = 5, 10, 15, …, T        (13.38)

Капитальные вложения и конечная продукция (в том числе для прироста уровня потребления) входит в (13.38) так же, как в (13.1). При этом  представляет собой кумулятивный прирост от начала планового периода, т.е. для t= 10, 15, ... величина  включает .

2.        Уравнения потребностей отраслей в основных производственных фондах:

, j ÎI, t = 5, 10, 15, …, T(13.39)

Уравнение (13.39) существенно отличается от формулировавшихся ранее соотношений по основным производственным фондам. Здесь:  — основные производственные фонды в j-й отрасли на конец года t, - — "гипотетический" коэффициент фондоемкости (соответствующий гипотезе, что не будет корректирующей его взаимозаменяемости между основными фондами и трудовыми ресурсами), s_j(t) и r_j(t) -объемы основных фондов, направляемых на изменение фондовооруженности труда.

3.         Уравнения потребностей отраслей в капитальных вложениях за пятилетний период:

,

j Î I; t = 5, 10, …, T; l = 1, 2, …,l_k (т.е. t = 5l, T = 5l_k)      (13.40)

где  — коэффициент пересчета ввода основных фондов в объем капитальных вложений;  — коэффициент дожития фондов, действовавших на начало пятилетки; N_j(t) — незавершенное строительство на конец года t. Предполагается, что незавершенное строительство составляет определенную долю от производственных капитальных вложений: N_j(t)=v^tu_j(t).

4. Уравнения капитальных вложений в последнем году пятилетия:

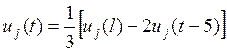, jÎ I, t = 5, 10, …, T, l = 1, 2, …, l_k. (13.41)

Посредством уравнений (13.41) связываются объемы капитальных вложений за пятилетие и в последнем году пятилетия. Используется гипотеза о линейном росте капиталовложений по годам пятилетия.

5.  Балансы трудовых ресурсов по отраслям:

, jÎ I, t= 5, 10, …, T(13.42)

где L_j(t) — численность занятых в j-й отрасли в году t;  — "гипотетический" коэффициент трудоемкости продукции;  — коэффициент взаимозаменяемости трудовых ресурсов и основных производственных фондов в j-й отрасли за пятилетие l (экономия живого труда за счет увеличения основных фондов).

6.  Критерий и условия роста уровня потребления по пятилетиям:

t = 5, 10,…, Т, l=1, 2, ....,1_k.(13.43)

Максимизируется общий прирост уровня потребления за плановый период (T лет) при условиях, регулирующих динамику роста потребления по пятилетиям. Для обеспечения более равномерного развития по пятилетиям модель включает ряд дополнительных ограничений: условия неубывания капитальных вложений по пятилетиям, минимальные доли капитальных вложений в конечном продукте по пятилетиям и т.п.

Экспериментальные расчеты по модели проводятся на 10-летний период (два пятилетия). В решении оптимизационной модели уровень всех основных экономических показателей оказывается выше, чем в вариантах развития народного хозяйства, рассчитываемых с помощью балансовой модели при использовании той же базы данных. Выше оказывается и уровень фондовооруженности труда. Расчеты показывают эффективность развития по трудосберегающему направлению (с положительным s_j) таких отраслей, как угольная промышленность, машиностроение, лесная промышленность, сельское хозяйство, строительство; а по фондосберегающему направлению — черной металлургии, электроэнергетики, химической промышленности и некоторых других.