Анализ производственных способов

4.5. Анализ производственных способов

Производственные способы и их сочетания. Понятие «производственный способ» является, с одной стороны, конкретизацией понятия «вид деятельности», введенного в гл. 3 при анализе общей модели народного хозяйства; с другой — это обобщение линейных однородных функций затрат.

Интенсивность применения способа ψ будем обозначать как x_ψ; эта интенсивность может измеряться объемом какого-либо выпускаемого продукта, какого-либо затрачиваемого ресурса и т.п. Каждому способу ψ соответствует вектор Аψ = (), компонентами которого являются коэффициенты выпуска продукции (со знаком «плюс») и затраты различных видов продукции и ресурсов (со знаком «минус»). Очевидно, невозможно произвести какой-либо продукт, не затратив других ресурсов или продуктов. С другой стороны, способы, в которых продукция вообще не выпускается, не могут найти применения. Поэтому в каждом векторе — используемом в народном хозяйстве производственном способе — обязательно содержатся как положительные, так и отрицательные компоненты.Выбор единицы изменения интенсивности влияет на абсолютные значения коэффициентов , но не влияет на их соотношения.

Совокупность производственных способов образует матрицу А = (); sÎM, ψ Î N. Как правило, в производстве могутодновременно применяться несколько способов (свойство аддитивности). При этом обычно предполагается, что характеристики одного способа не зависят от применения других способов (свойство автономности). Из этих двух свойств следует, что линейные комбинации базовых способов образуют новые способы. Например, если А₁, А₂, … , A_k — базовые способы, то 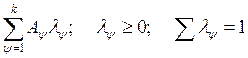 дает новый способ. Однако способы, являющиеся линейными комбинациями базовых способов, не имеет смысла непосредственно включать в условия оптимизационной модели, так как они формируются автоматически в процессе решения.

Общие результаты функционирования всех способов по каждому ингредиенту s выражаются суммой . Разобьем множество всех ингредиентов на два подмножества: продукты и воспроизводимые ресурсы s₁ÎM₁ и невоспроизводимые ресурсы s₂ÎM₂. Тогда означает выпуск конечной продукции вида s₁  (т.е. разность произведенной и использованной продукции в сфере производства) , а - общие затраты невоспроизводимого ресурса s₂ (при этом поменяем знаки коэффициентов так, чтобы ).

Обозначив объем конечной продукции вида s₁,  — наличные ресурсы вида s₂, получаем основные ограничения линейной модели производства:

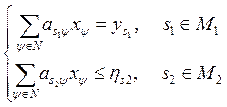              (4.39)

Система уравнений и неравенств (4.39) является конкретизацией соответствующих условий общей модели оптимального планирования. Они включаются во всякую линейную статическую модель народного хозяйства.

Анализ однопродуктовых способов. Рассмотрим особенности производственных способов, в каждом из которых изготавливается только один продукт. Интенсивности применения таких способов естественно измерять объемом выпуска продукта. Вектор А_ψ в этом случае включает только одну положительную компоненту (единицу выпускаемого продукта); все остальные компоненты — отрицательные и нулевые.

Поскольку способы производства аккумулируют самые разнообразные признаки дифференциации производственных условий (по технологии, организации, взаимозаменяемости ресурсов и т.п.), то число способов (даже для одного продукта) может быть очень велико. Поэтому актуальна задача отбора только эффективных способов.

!!!!!!!!

нологии, организации, взаимозаменяемости ресурсов и т.п.), то число способов (даже для одного продукта) может быть очень велико. Поэтому актуальна задача отбора только эффективных способов.

Введем понятие абсолютно неэффективного способа. Пусть в сравниваемых способах производится продукт s₀. Коэффициенты затрат  будем рассматривать по абсолютной величине (со знаком «плюс»). Способ φ производства продукта s₀ абсолютно неэффективен, если существует какой-либо другой способ или выпуклая комбинация других способов, при которых равный выпуск продукта осуществляется при меньшем потреблении хотя бы одного ресурса и не большем потреблении других ресурсов.

Задача выявления абсолютно неэффективных способов в общем случае сводится к доказательству совместности системы из m неравенств и уравнений. Однако существуют и более простые правила. В частности, абсолютно неэффективным является всякий способ φ, в котором все коэффициенты затрат не меньше, чем соответствующие коэффициенты какого-либо другого способа ω, и хотя бы один коэффициент больше, т.е.  (одно из неравенств выполняется как строгое).