экономической динамики, позволяя существенно сокращать эмпирическую работу по их построению и анализу.
11.1. Динамические межотраслевые модели
Отличительный признак теоретических межотраслевых динамических моделей — описание соотношений "затраты — выпуск" в форме матриц межотраслевого баланса, где каждый вид продукции представлен только одним производственным способом, а в каждом способе выпускается только один продукт. Место динамических межотраслевых моделей среди моделей экономической динамики определяется тремя моментами. Во-первых, они являются детализированными (дезагрегированными) аналогами моделей воспроизводства общественного продукта и национального дохода (см. 10.1, 10.2). Во-вторых, они представляют собой обобщения статических (балансовых и оптимизационных) межотраслевых моделей (см. гл. 6, 8). В-третьих, они служат теоретико-методологической основой прикладных динамических моделей с матрицами межотраслевого баланса (см. гл. 13).
Динамическая модель В.Леонтьева. Предложенная В.Леонтьевым в начале 50-х гг. динамическая межотраслевая модель является классическим примером использования систем дифференциальных уравнений в исследовании проблем экономического роста. Построение этой модели удобно представить как дезагрегирование элементов простейшей динамической модели воспроизводства общественного продукта (см. 10.1), при котором эндогенные и экзогенные макропеременные заменяются векторами, а технологические макропараметры — матрицами. Модель имеет вид
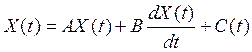 (11.1)
(11.1)
где ![]() - вектор-столбец объемов производства;
- вектор-столбец объемов производства;
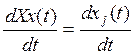 — вектор-столбец абсолютных приростов
производства;
— вектор-столбец абсолютных приростов
производства;
c(t) — вектор-столбец потребления (включая непроизводственное накопление);
![]() - матрица коэффициентов прямых материальных
затрат (в
отличие от коэффициентов статического межотраслевого баланса коэффициенты в
динамической модели включают также затраты на возмещение выбытия и капитальный ремонт
основных производственных фондов);
- матрица коэффициентов прямых материальных
затрат (в
отличие от коэффициентов статического межотраслевого баланса коэффициенты в
динамической модели включают также затраты на возмещение выбытия и капитальный ремонт
основных производственных фондов);
![]() - матрица коэффициентов
капиталоемкости приростов производства (затраты производственного накопления на единицу прироста
соответствующих видов продукции; смысл этих коэффициентов будет уточнен ниже); i, jÎI, I={1, …, n}. Поскольку
- матрица коэффициентов
капиталоемкости приростов производства (затраты производственного накопления на единицу прироста
соответствующих видов продукции; смысл этих коэффициентов будет уточнен ниже); i, jÎI, I={1, …, n}. Поскольку 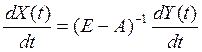 , то вместо (11.1) может исследоваться система
дифференциальных уравнений
, то вместо (11.1) может исследоваться система
дифференциальных уравнений
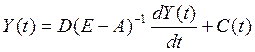 . (11.2)
. (11.2)
где В(Е — А)-1 — матрицакоэффициентовполной приростной капиталоемкости, т.е. полных затрат производственного накопления на единичные приросты элементов используемого национального дохода[1].
Предполагается, что матрица А продуктивна. В дальнейшем анализе удобно считать матрицу А неразложимой, а матрицу В — невырожденной (см. разъяснения в ДМНХ, с. 124). Тогда (Е - А)-1 > Е + А, В (Е - А)-1 >В.
Очевидно,
что экономический смысл имеют только решения X(t) ³0. Как будет показано
далее, экономическим предпосылкам модели (11.1) соответствуют только неубывающие
траектории X(t), т.е. 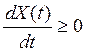 .
.
Решение
системы (11.2) при 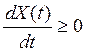 в силу неотрицательности матриц (Е-А)-1
и В(Е - А)-1 гарантирует, что
в силу неотрицательности матриц (Е-А)-1
и В(Е - А)-1 гарантирует, что
Y(t) ³ 0, X(t) ³ 0, 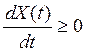
В соответствии с теорией дифференциальных уравнений решение систем (11.1) и (11.2) проводится в три этапа: а) определяется общее решение однородной системы уравнений при c(t) = 0; б) находится частное решение неоднородной системы; в) из начальных условий рассчитываются неопределенные постоянные общего решения.
Динамика замкнутой производственной системы. Проанализируем систему однородных уравнений:
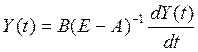 (11.3)
(11.3)
Решение этой системы характеризует предельные технологические возможности развития производства при заданных матрицах А и В, когда все ресурсы национального дохода направляются на расширенное воспроизводство. Такая же ситуация на примере макромодели исследовалась в 10.1.
Естественно,
возникает вопрос: существует ли траектория системы (11.3) ![]() с постоянным темпом прироста m, одинаковым для всех компонент
с постоянным темпом прироста m, одинаковым для всех компонент
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.