13.2. Рекурсивные модели
Наиболее известные и близкие друг другу динамические межотраслевые модели рекурсивного типа были разработаны в середине 60-х гг. в ИЭиОПП СО АН СССР (Н.Ф.Шатиловым)и НИЭИ при Госплане СССР (Ф.Н.Клоцвогом).
В настоящее время модель НИЭИ включена в систему расчетов народнохозяйственного плана под названием "укрупненная динамическая модель межотраслевого баланса в стоимостном выражении" (см. [5. с. 88-95]).
Данная модель разрабатывается в стоимостном выражении в разрезе 18 — 25 отраслей производства. Она включает три типа балансовых уравнений: балансы производства и распределения продукции, балансы основных фондов и баланс трудовых ресурсов.
1. Балансы производства и распределения продукции:
![]() i Î I (13.1)
i Î I (13.1)
При этом ![]() - прочая
конечная продукция.
- прочая
конечная продукция.
Таким образом, (13.1) образуется путем сочетания соотношений статической
межотраслевой модели и упрощенного соотношения (12.2). Коэффициенты ![]() характеризуют
материально-вещественную структуру капитальных вложений (расход продукции
машиностроения и строительства на 1 млн. руб. капитальных вложений в j-ю отрасль).
характеризуют
материально-вещественную структуру капитальных вложений (расход продукции
машиностроения и строительства на 1 млн. руб. капитальных вложений в j-ю отрасль).
2. Балансы основных производственных фондов по отраслям-потребителям:
![]() ,(13.2)
,(13.2)
При этом ![]() .
.
Таким образом, равенства (13.2) объединяют в несколько измененном виде условия (12.7), (12.8), (12.13). Здесь следует отметить две особенности.
Объемы основных фондов непосредственно балансируются только по
отраслям-потребителям. Предполагается, что материально-вещественный состав фондов (по
элементам ![]() ) балансируется коэффициентами
) балансируется коэффициентами ![]() и
и ![]() .
Основные фонды не приводятся к среднегодовым. Потребности и ресурсы фондов
рассчитываются на конец года; т.е. по сравнению с обозначениями
.
Основные фонды не приводятся к среднегодовым. Потребности и ресурсы фондов
рассчитываются на конец года; т.е. по сравнению с обозначениями ![]() в
12.2 здесь имеется сдвиг на один год.
в
12.2 здесь имеется сдвиг на один год.
Из (13.2) получаем, что необходимый ввод в действие основных производственных фондов в году tсоставляет
![]() (13.3)
(13.3)
Связь производственных капитальных вложений и ввода основных производственных фондов, представленная в гл. 12 соотношением (12.2), в рассматриваемой модели имеет вид
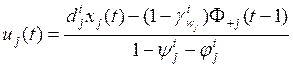 (13.4)
(13.4)
где ![]() - — норма прироста задела
незавершенного строительства;
- — норма прироста задела
незавершенного строительства; ![]() — доля прочих
капитальных вложений (не связанных с вводом фондов) в общем объеме
производственных капитальных вложений.
— доля прочих
капитальных вложений (не связанных с вводом фондов) в общем объеме
производственных капитальных вложений.
3. Баланс трудовых ресурсов:
![]() . (13.5)
. (13.5)
Ставится условие обязательного использования трудовых ресурсов.
Общее число условий (13.1), (13.3) - (13.5) равно 3п + 1. При этом равенства (13.3) выполняют роль
уравнений-определений. Они используются для
расчета ввода фондов ![]() после нахождения объемов производства. При подстановке (13.4) в
(13.1) получаем для года tсистему из п +
1 уравнений, содержащую п + 1 неизвестных xj(t),
после нахождения объемов производства. При подстановке (13.4) в
(13.1) получаем для года tсистему из п +
1 уравнений, содержащую п + 1 неизвестных xj(t), ![]() .
.
Модель может дополняться условием, регулирующим долю производственных капитальных вложений в конечном общественном продукте:
![]() (13.6)
(13.6)
Оно связывает результаты межотраслевой модели с расчетами по макроэкономическим моделями балансу народного хозяйства.
Расчеты по модели организуются в следующем порядке. На начало года t= 1 известны объемы фондов Ф+j(0). Решается система уравнений для t= 1 и находятся величины Ф+j(1) = Ф+j(0) + DФ+j(1) - W+j(1). Затем переходим к задаче для года (t + 1) и т.д.
Рассматриваемая модель используется на разных стадиях разработки перспективного плана. На предварительной стадии при помощи модели уточняются общеэкономические показатели, полученные на основе макроэкономических моделей и расчетов балансов народного хозяйства. В процессе вариантных расчетов исследуется влияние различных направлений структурной политики и динамики эффективности производственных ресурсов на темпы и пропорции развития. На стадии разработки основных направлений экономического и социального развития страны с помощью модели уточняются и балансируются проектировки развития отдельных отраслей производства.
Модель динамического межотраслевого баланса Н.Ф.Шатилова и ее многочисленные обобщения используются в предплановых исследованиях[1]. Отличия основного варианта модели от рассмотренной выше рекурсивной динамической модели заключаются в следующем: 1) балансы производства и распределения продукции строятся отдельно по продукции I и II подразделений; 2) балансы основных производственных фондов даются как по отраслевой принадлежности, так и по вещественному составу, то есть по элементам Фij, iÎ I1, j Î I; 3) выбор объемов и структуры потребления осуществляется с помощью "шкалы потребления", позволяющей выбирать лучший вариант потребления при совместности всех других условий (подробный анализ основной модели и ее модификаций см. в ДМНХ, с. 200-205, [8], [11]).
[1] Н.Ф.Шатилов (1931 — 1977) — автор ряда крупных работ по теории расширенного социалистического воспроизводства. Созданная им прикладная модель динамического межотраслевого баланса оказала заметное влияние на развитие и применение динамических моделей народного хозяйства.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.