Анализ производственных способов, страница 2

Сравнительно легко проверять способ на абсолютную неэффективность путем сопоставления его с выпуклой комбинацией двух других базовых способов. Так, способ φ является абсолютно неэффективным в том случае, если найдутся хотя бы два других способа ω₁ и ω₂, комбинация которых дает более эффективный способ:

(одно из неравенств выполняется как строгое). Обратимся к рис. 4.11. В пространстве затрат двух ресурсов изображены способы производства А, В, С, D, Е и две выпуклые изокванты, соответствующие равным объемам производства. Как видим, изокванты не проходят через точки E₁ и E₂. Это означает, что комбинации способов С и D позволяют произвести то же количество продукции с меньшими затратами обоих ресурсов. Следовательно, способ Е абсолютно неэффективен^[1].

Оптимальное сочетание производственных способов. Пусть один продукт производится несколькими способами. Каждый вид затрачиваемых ресурсов ограничен. Требуется максимизировать общий выпуск продукта.

Имеем задачу линейного программирования:

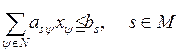            (4.40)

Попытаемся выявить свойства решений этой задачи, опираясь на теорию линейного программирования и теоретические положения о соизмерении затрат и результатов в оптимальном планировании (см. гл. 3).

Очевидно, что решение задачи (4.40) всегда существует (благодаря тому, что ≥ 0, b_s> 0). При этом оптимальный план может быть единственным или же число оптимальных планов бесконечно. В случае единственности оптимального плана число используемых производственных способов (имеющих x_ψ > 0) не может превосходить числа ресурсов (m). Поэтому чем больше ресурсов учитывается в задаче, тем больше способов может войти в оптимальный план.

Следует уточнить, что максимальное число положительных величин x_ψ > 0 не может превышать числа полностью используемых ресурсов. Это уточнение важно, поскольку в оптимальном плане задачи (4.40) не все ресурсы могут использоваться полностью. Экономически это объясняется тем, что в имеющихся способах производства взаимозаменяемость ресурсов недостаточна. Поэтому чем разнообразнее способы по соотношениям коэффициентов , тем больше число полностью используемых ресурсов. Таким образом, существует определенная зависимость между числом входящих в оптимальный план способов, числом учитываемых в задаче ресурсов, числом и дифференциацией способов.

Пусть X* - оптимальный план, включающий определенный набор производственных способов. При увеличении всех ресурсов в λ раз набор производственных способов не изменится, а интенсивность применения каждого способа и всего объема производства  увеличится в λ раз. Таким образом, модель (4.40) можно интерпретировать как особую форму однородной производственной функции первой степени. Эта форма записи производственной функции наглядно демонстрирует ее экстремальную природу.

Запишем задачу, двойственную к (4.40):

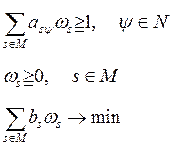            (4.41)

Решение задачи (4.41) всегда существует: W* = (w*_s). Как было показано в гл. 3, w*_s — оптимальная оценка s-ro ресурса, характеризующая предельную эффективность s-го ресурса. Из теории линейного программирования следует, что по мере увеличения b_s величина w*_s снижается (кусочно-постоянным образом), т.е. предельная эффективность ресурса уменьшается. Таким образом, решение задачи (4.40) при меняющемся параметре b_So (и фиксированных значениях всех других b_s) дает непрерывную кусочно-линейную функцию выпуска продукта от величины затрачиваемого ресурса s₀.

Нормы эквивалентной взаимозаменяемости ресурсов в оптимальном плане равны обратным соотношениям оптимальных оценок этих ресурсов: 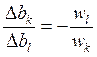. Для используемых в оптимальном плане способов выполняется равенство 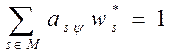. Если же способ не входит в оптимальный план, то . Разность  показывает, насколько уменьшится объем выпуска, если в оптимальный план принудительно ввести единицу продукта, производимого ψ способом.

Литература

1. Ашманов С.А. Введение в математическую экономику. М.: Наука, 1984. Ч. III. 1.

2. Клейнер Г.Б. Производственные функции. М.: Финансы и статистика, 1986.

3. Маленво Э. Лекции по макроэкономическому анализу. М.: Наука, 1985.

4. Павлов В.Н. Технологический прогресс и полезность средств производства.
Новосибирск: Наука, 1987.

5. Плакунов М.К., Раяцкас Р.Л. Производственные функции в экономическом
анализе. Вильнюс: Минтиc, 1984.