



Алгоритм
1.1 Назначение алгоритма
Алгоритм
предназначен для оптимальной группировки исходных данных на группы (таксоны) в
пространстве показателей ![]() . Группировка
осуществляется на различное количество групп в некотором диапазоне. В каждую
группу объединяются "похожие" по описанию X реализаций. Подсчитывается модифицированный критерий
Фишера из дисперсионного анализа, позволяющий определить также и наилучшее
количество групп при таксономии.
. Группировка
осуществляется на различное количество групп в некотором диапазоне. В каждую
группу объединяются "похожие" по описанию X реализаций. Подсчитывается модифицированный критерий
Фишера из дисперсионного анализа, позволяющий определить также и наилучшее
количество групп при таксономии.
1.2 Описание алгоритма
Имеется
матрица исходных данных ![]() , где NO – объем выборки, a NP - общее количество показателей (входных и выходных).
Необходимо для каждого значения числа групп K в заданном диапазоне
, где NO – объем выборки, a NP - общее количество показателей (входных и выходных).
Необходимо для каждого значения числа групп K в заданном диапазоне ![]() осуществить
разбиение NO исходных объектов на K групп так, чтобы в каждую группу
вошли объекты, имеющие сходные (в среднем) значения показателей
осуществить
разбиение NO исходных объектов на K групп так, чтобы в каждую группу
вошли объекты, имеющие сходные (в среднем) значения показателей ![]() . Необходимо также рассчитать дисперсионные
критерии качества группировки при различных значениях K с целью выбора исследователем и
наилучшего значения K.
. Необходимо также рассчитать дисперсионные
критерии качества группировки при различных значениях K с целью выбора исследователем и
наилучшего значения K.
Задача в целом решается по следующей схеме:
1) вычисляется среднеквадратическое
отклонение значений каждого из NP исходных факторов ![]() ;
;
2) вычисляется матрица NOх NO взаимных "расстояний" между исходными объектами;
3) для каждого значения числа групп K в диапазоне ![]() группирование
начинается со случайного выбора K из NO исходных объектов в качестве
"центров классов";
группирование
начинается со случайного выбора K из NO исходных объектов в качестве
"центров классов";
4) все NO исходных объектов перераспределяются по группам по принципу "ближайшего центра";
5) во вновь сформированных группах заново определяются "центральные" объекты;
6) пункты 4-5 последовательно повторяются до тех пор, пока объекты не перестанут перераспределяться;
7) при заданном K результаты получившейся группировки объектов печатаются;
8) для каждого K печатаются значения дисперсионных критериев качества группировки.
1.3 Математическая постановка и описание алгоритма
Дано:
- ![]() - матрица исходных данных, где NO - число объектов, а NP - общее число всех факторов;
- матрица исходных данных, где NO - число объектов, а NP - общее число всех факторов;
- информация о типе (количественный или дискретный) каждого Xj;
-
априорный информационный вес Wj для каждого ![]() ;
;
- указатель типа метрики - евклидова норма или средне-модульное расстояние.
Требуется осуществить такое распределение NO исходных объектов по K классам, чтобы минимизировать
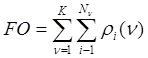 , (1)
, (1)
где ![]() - число объектов в
- число объектов в ![]() -м таксоне, а
-м таксоне, а ![]() (
(![]() ) - расстояние i-го объекта
) - расстояние i-го объекта ![]() -го таксона до „центрального”
объекта этого таксона. Под „центральным” объектом понимается тот
из
-го таксона до „центрального”
объекта этого таксона. Под „центральным” объектом понимается тот
из ![]() объектов, для которого величина
объектов, для которого величина 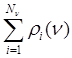 минимальна.
Центральный объект наиболее близок к «центру тяжести» таксона.
минимальна.
Центральный объект наиболее близок к «центру тяжести» таксона.
Расстояние
![]() вычисляется в евклидовой метрике
вычисляется в евклидовой метрике
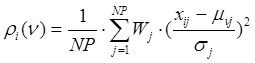 , (2)
, (2)
где
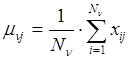 , (3)
, (3)
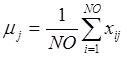 , (4)
, (4)
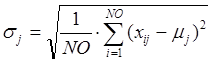 , (5)
, (5)
или согласно среднемодульному принципу
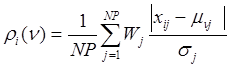 (6)
(6)
формулы (1) и (6) справедливы
лишь для количественных ![]() .
.
Если
какой-то x![]() дискретный, то соответствующее
слагаемое в формулах (1) и (6) имеет вид
дискретный, то соответствующее
слагаемое в формулах (1) и (6) имеет вид
ì 0, при x![]()
![]() = í
= í
î W![]() , при x
, при x![]()
Здесь уже ![]() - значение j-й
координаты у «центрального» объекта
- значение j-й
координаты у «центрального» объекта ![]() -й группы.
-й группы.
Нетрудно видеть, что значение F0 при увеличении монотонно убывает. Для сравнения между собой качества результатов таксономии при различных значениях К воспользуемся критерием дисперсионного анализа, который имеет вид:
F=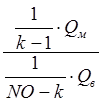 , (7)
, (7)
Здесь
Q![]() - величина межгруппового разброса, a Q
- величина межгруппового разброса, a Q![]() - величина среднего внутригруппового разброса реализации. При конкретном
значении K имеем Q
- величина среднего внутригруппового разброса реализации. При конкретном
значении K имеем Q![]() = FO(K), и Q
= FO(K), и Q![]() F(K). Здесь FO(1) и FO(K) - значения критерия FO, определенные по (1) при К =1 и при заданном
значении соответственно. Чем больше F, тем выше качество таксономии. В качестве другого
обобщенного критерия качества таксономии может быть взята относительная
разность величины F и критического
значения F
F(K). Здесь FO(1) и FO(K) - значения критерия FO, определенные по (1) при К =1 и при заданном
значении соответственно. Чем больше F, тем выше качество таксономии. В качестве другого
обобщенного критерия качества таксономии может быть взята относительная
разность величины F и критического
значения F![]() определенному по таблицам распределения
Фишера при (K - I) и (NO - K) степенях свободы и заданной доверительной
вероятности
определенному по таблицам распределения
Фишера при (K - I) и (NO - K) степенях свободы и заданной доверительной
вероятности ![]() (в программе
(в программе ![]() =0,95):
=0,95):
FD=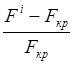 (8)
(8)
Чем больше FD, тем выше качество таксономии.
При заданном числе групп К алгоритм реализует итерационную процедуру локальной оптимизации критерия качества
Для повышения качества решения в программе реализуется (IR • К) различных локальных оптимизаций при одном K с выбором наилучшего решения, величина IR задается.
Значения
F - наилучших группировок при разных K запоминаются. В конце решения
задачи рассчитываются и печатаются величины ![]() для
различных значений К.
для
различных значений К.
Окончательно
следует выбирать тот вариант группировки (то значение K), при котором величины ![]() максимальны.
максимальны.
Программа обеспечивает такое распределение объектов по K классам, чтобы минимизировать FO - сумму межклассовых и внутриклассовых расстояний между объектами ri (V).
Алгоритмом предусматривается последовательное оптимальное разбиение совокупности районов на К = 2, 3, 4, 5 и т. д. классов. Качество таксономии каждый раз оценивается двумя критериями:
F - критерий дисперсионного анализа;
FD - обобщенный критерий таксономии, учитывающий число степеней свободы системы и заданную доверительную вероятность g (задана g = 0,95).
Чем выше значения критериев F и FD, тем выше качество таксономии.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.