Алгоритм для группировки объектов выборки в группы и вычисления статистических характеристик каждой группы и выборки в целом

Алгоритм

1.1 Назначение алгоритма

Алгоритм предназначен для группировки объектов выборки в группы и вычисления статистических характеристик каждой группы и выборки в целом.

1.2 Содержательная постановка задачи и расчетная схема

Имеется совокупность NO объектов . Функционирование каждого объекта описывается рядом количест­венных признаков . Один из этих признаков   является зависимым от остальных ,  .

Форма зависимости известна. Необходимо определить теорети­ческие значения зависимого признака (Y*) для каждого объекта выборки и сгруппировать по нему объекты в группы. Границы групп (по выравненному Y*) заданы. Для каждой группы и выборки в целом определить статистические характеристики. Решение осуществляется на основе исходной матрицы данных X(NO, NP) по следующей схеме:

а) среди признаков, характеризующих объекты выборки, устанавливается зависимый (Y);

б) задается вид уравнения многофакторной регрессии;

в) задаются число групп и границы каждой по теоретичес­кому значению зависимого признака Y;

г) по заданному уравнению регрессии и фактическим значениям  определяются теоретические значения за­висимого признака (Y*) для каждого объекта выборки;

д) по выравненному Y * объекты группируются;

е) для каждой группы устанавливаются номера объектов, вошедших в группу, фактическое и выравненное значение зависимого признака, отклонение выравненного значения от факти­ческого, среднемодульная ошибка аппроксимации зависимого признака;

ж) для выборки в целом определяются среднее значение каждого признака, среднее значение зависимого признака, среднемодульная ошибка аппроксимации зависимого признака.

1.3 Математическая постановка и описание алгоритма

Пусть значение ,  характеризует i-й объект выборки . Форма  зависимости    задана   уравнением:

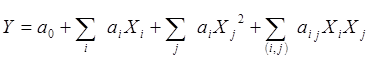
,                                                                                                                      (1)

где Y* - теоретическое значение зависимого признака;

       X_j - фактическое значение независимой переменной, j = 1,…, NP;

        - коэффициенты регрессии.

Задано число групп (KG) и нижняя граница B (KG) каждой группы по выравненному значению зависимого признака (Y*).

Определить вектор , среднее значение зависимого признака , среднемодульную ошибку аппроксимации зависимого признака , среднее значение не­зависимого признака  для выборки в целом. Сгруппировать объекты в группы, определить номера объектов, вошедших в группу, среднемодульную ошибку аппрок­симации зависимого признака в группе. Вектор   определяется по формуле.

Среднее значение зависимого признака  определяется по формуле:

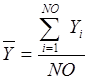         ,                                                                                           (2)                                                                                                      где    NO - число   объектов выборки;

Y_i - фактическое значение зависимого признака для i-го объекта.

Среднемодульная ошибка аппроксимации зависимого при­знака                            определяется по формуле

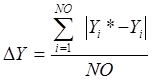,                                                                                                                                                                     (3)

где  - теоретическое значение зависимого признака для i-го объекта.

Среднее значение независимого признака  определяется по формуле

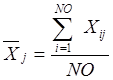,                                                                                                                                                                           (4)

где  - фактическое значение j-го признака для i-го объекта.

Пусть - нижняя граница K-ой группы объектов по выравненному значению Y*,  - нижняя граница следующей по порядку -ой группы. Тогда в группу K войдут те объекты, для которых .

Среднемодульная ошибка аппроксимации зависимого признака Y в K-й  группе  определяется по формуле

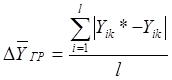,                                                                                                                                                                 (5)

где l - число объектов, вошедших в K -ю группу;

       - теоретическое значение зависимого признака для объекта i в группе K.