Алгоритм для вычисления и анализа тесно­ты и характера парных корреляционно-регрессионных связей между факторами исходной информации, выбора значимых и удале­ние малозначимых мулътиколлинеарных факторов - аргументов

Алгоритм

1.1 Назначение алгоритма

Алгоритм предназначен для вычисления и анализа тесно­ты и характера парных корреляционно-регрессионных связей между факторами исходной информации, выбора значимых и удале­ние малозначимых мулътиколлинеарных факторов - аргументов. Рассчитываются показатели тесноты связи, критерии значимос­ти связей и кривизны зависимостей.

1.2 Содержательная постановка и расчетная схема

Имеется выборка N объектов (наблюдений, реализаций). Каждый из них количественно описан системой входных (аргумен­ты, факторы)  выходных (результирующие показатели)  признаков, составляющих массив исходной информации . Предполагается, что информация предварительно проанализиро­вана и, при необходимости, удалены нетипичные объекты, про­верены и откорректированы аномальные наблюдения.

Требуется:

а) дать обобщенный анализ тесноты и характера парных связей между всеми признаками;

б) выявить факторы, не представляющие интереса для последу­ющих этапов моделирования и изучения соответствующих про­цессов, явлений.

Поставленная задача реализуется в алгоритме по определенной схеме и представляется в виде выдаваемых на печать параметров, критериев и статистических оценок.

1. Рассчитываются показатели тесноты парной линейной  и нелинейной  связи между всеми признаками выбор­ки.

2. Оценивается значимость корреляционных связей, для чего вычисляются значения  критериев (Стьюдента) коэффи­циентов корреляции .

3. Оценивается характер парных зависимостей, для чего вы­числяются F -критерии (Фишера) кривизны.

 Анализируются и выделяются пары слабо связанных призна­ков, значения  и  для которых не превышают назначенные пороговые величины  и .

5. На основе анализа корреляционных связей одним из двух способов (алгоритмов) устанавливаются мультиколлинеарные факторы, а из них те факторы, которые подлежат удале­нию.

1.3 Математическая постановка и описание алгоритма

Дано:

 - матрица факторов;

где  - число факторов;

       - число наблюдений (объектов).

Требуется:

I. Вычислить парные корреляционные связи между факторами - коэффициенты корреляции линейных парных зависимостей  и коэффициенты корреляционных отношений,

где j - номер фактора-функции ;

      k - номер фактора-аргумента , номер фактора-аргумента всегда больше номера фактора-функции .

2. Вычислить критерии значимости   и критерии кри­визны нелинейных зависимостей  всех пар рассматриваемых X.

3. Исключить малозначимые X. Исключаются те аргументы  для которых имеет место одно из двух неравенств:

,                                                                                          (1)

,                                                                                         (2)

где  и  - минимальный и максимальный уровни тес­ноты парной связи между  и , задаваемые по желанию исследователя.

 Исключить мультиколлинеарные X. Исключается часть аргументов  из группы  тех, для каждого из которых имеет место хотя бы одно неравенство.

                                                                                (3)

где  - максимальный уровень тесноты парной связи между аргументами, задаваемый исследователем. Значения  ,  и  рассчитываются по из­вестным формулам математической статистики.

При расчетах используются:

средние арифметические каждого фактора

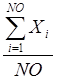= ,                                                                                                   (4)

где  - фактическое значение фактора;

       - номер наблюдения в выборке;

       - число наблюдений.

Средние квадратические отклонения каждого фактора

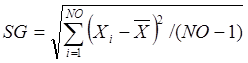;                                                                             (5)

коэффициенты корреляции для каждой пары факторов рассчиты­ваются по формуле

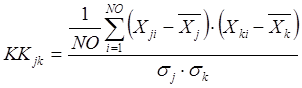.                                                                     (6)

Значимость коэффициентов корреляции оценивается по Т-критерию

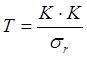,                                                                                                     (7)

где - среднее квадратическое отклонение коэффициента корреляции.

Критерий Т имеет распределения Стьюдента с числом степеней свободы . Корреляционная связь при­знается значимой, если расчетное значение критерия больше табличного, взятого с заданным доверительным уровнем.

Корреляционное отношение рассчитывается для криво­линейной зависимости типа "квадратная парабола" по формуле:

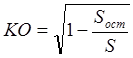,                                                                                              (8)

где  - остаточная дисперсия фактора-функции,

      S - полная дисперсия фактора-функции.

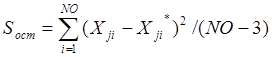,                                                                        (9)

где  фактическое значение -го фактора-функции;

      значение -го фактора-функции, определенное по формуле регрессии.

Значимость криволинейной зависимости определяется по формуле

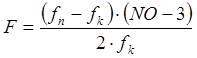,                                                                                  (10)

где  и  - сумма квадратов разностей значений, рассчитанных по линейной и криволиней­ной зависимостям.

Критерий  имеет распределение Фишера со степенями свободы  и . При совпадении линейной и криволинейной моделей расчетный критерий меньше табличного, взятого с доверительным уровнем.

Блок "удаление" в программе "Матрица парных связей" для каждой заданной признак-функции () выявляет, ана­лизирует и исключает из дальнейшего рассмотрения малозна­чимые и мультиколлинеарные факторы-аргументы ().

По желанию исследователя это осуществляется в про­грамме одним из двух способов.

I. Среди групп  неудаленных аргументов находится пара  и . наиболее тесно связанных:

,.                                                  (11)

Из двух факторов  и  исключается наименее связанный с , то есть на котором достигается

,    .                                                                           (12)

2. Определим величину  как число аргументов  из , для которых имеет место неравенство (3). Тогда из двух аргументов  и , найденных по формуле (11) исключается тот, на котором достигается

 , .                                                                                        (13)

В случае равенства  исключается из двух аргументов тот, на котором достигается (12).

Процесс нахождения пар аргументов  и  и исклю­чения одного из них одним из двух способов продолжается до тех пор, пока имеются пары аргументов  и , для кото­рых имеет место неравенство (3).