решения методом Монте-Карло, поскольку высокое быстрое действие компьютеров обеспечивает возможность многократного повторения случайных испытаний и последующую обработку полученных данных.
Опишем алгоритм решения методом Монте-Карло системы линейных уравнений [6]. Пусть исходная система (1.1) записана в виде:
a11x1 + a12x2 + … + a1nxn + a1n + 1 = 0
a21x1 + a22x2 + … + a2nxn + a2n + 1 = 0 (2.1)
……………………………………
an1x1 + an2x2 + … + annxn + ann + 1 = 0
Приведем систему (2.1) к виду, обычно используемому для применения метода итераций:
x1 = a11x1 + a12x2 + a13x3 + … + a1nxn + a1n + 1
x2 = a21x1 + a22x2 + a23x3 + … + a2nxn + a2n + 1 (2.2)
……………………………………………….
xn = an1x1 + an2x2 + an3x3 + … + annxn + ann + 1
Будем предполагать, что для системы (2.2) имеют место соотношения:
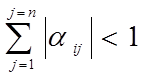 . (i = 1, 2, …, n) (2.3)
. (i = 1, 2, …, n) (2.3)
От системы (2.1) к системе (2.2), удовлетворяющей соотношениям (2.3), можно перейти с помощью таких преобразований.
Пусть для фиксированного i
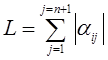 .
(2.4)
.
(2.4)
Если в i-м уравнении системы (2.1) коэффициент aii>0, то делим каждый член этого уравнения на –L, в противном случае делим каждый член уравнения на L.
Обозначим
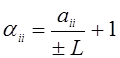 и
и 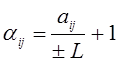 .
(2.5)
.
(2.5)
Полученные числа и будут коэффициентами системы (2.2).
Сопоставим теперь i-му уравнению этой системы разбиение отрезка [0; 1] на n + l отрезков точками sj, каждая из которых мест координату, определяемую соотношениями
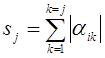 (j = 1, 2, ..., n). (2.6)
(j = 1, 2, ..., n). (2.6)
Кроме того, положим s0 = 0 и sn+1 = 1.
Рассмотрим процесс «случайного блуждания» некоторой частицы, которая в начальный момент находится в точке s, i-го разбиения отрезка [0; 1]. Воспользовавшись возможностью получения случайных чисел, равномерно распределенных на отрезке [0; 1], рассмотрим такое случайное число c. Если оно удовлетворяет соотношению
sj – 1< c ≤ sj (j = 1, 2, ..., n) (2.7)
для точек рассматриваемого i-го разбиения, то считаем, что частица
переходит из точки si i-го
разбиения в точку sj j-го
разбиения. Снова получаем случайное число и рассматриваем его положение
относительно точек j-го
разбиения. Если в этом разбиении полученное число лежит на отрезке ![]() , то считаем, что частица переходит из точки sj j-го
разбиения в точку sk k-го разбиения. В том случае, когда для
некоторого разбиения очередное случайное число попадет на отрезок
, то считаем, что частица переходит из точки sj j-го
разбиения в точку sk k-го разбиения. В том случае, когда для
некоторого разбиения очередное случайное число попадет на отрезок ![]() считаем, что частица переходит в точку sn+1 и процесс случайного блуждания
заканчивается. Последовательность точек si, sj, sk, ..., sl, sm, sn+1 назовем траекторией частицы. Свяжем
с этой траекторией случайную величину yi, задаваемую соотношением
считаем, что частица переходит в точку sn+1 и процесс случайного блуждания
заканчивается. Последовательность точек si, sj, sk, ..., sl, sm, sn+1 назовем траекторией частицы. Свяжем
с этой траекторией случайную величину yi, задаваемую соотношением
![]() ,
(2.8)
,
(2.8)
где
![]() ,
, ![]() , ...,
, ..., ![]() , (2.9)
, (2.9)
а величина ![]() определяется
равенством
определяется
равенством
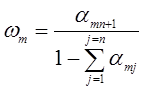 . (2.10)
. (2.10)
Можно доказать, что математическое ожидание случайной величины yi, равно значению корня xi системы (2.2). Этот факт дает способ практического отыскания xi. Осуществим M реализаций случайного блуждания частицы по траектории, начинающейся в точке si. Обозначим через Y сумму значений случайной величины yi, полученных во всех реализациях. Тогда будем иметь приближенное равенство
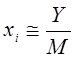 .
(2.11)
.
(2.11)
Следует иметь в виду, что при решении систем линейных уравнений методом Монте-Карло точность получаемых результатов сравнительно невысока. Повышение точности вычислений требует значительного увеличения числа реализаций, а значит, и времени решения системы. Вместе с тем ни один из известных методов решения систем линейных уравнений (кроме метода Монте-Карло) не позволяет вычислить значение одного корня системы, не вычисляя значения других корней.
3 Решение систем линейных уравнений методом ортогонализации
Очень часто программа решения системы линейных уравнений должна быть использована не для решения одной, отдельно взятой системы, а как составная часть более общей программы. Естественно, что «встраиваемая» программа должна быть как можно компактнее, не должна требовать никаких проверок сходимости или значительных преобразований исходной, системы. Поэтому опишем сейчас еще один метод решения системы линейных уравнений – метод ортогонализации.
Пусть исходная система записана в виде:
a11x1 + a12x2 + … + a1nxn + a1n + 1 = 0
a21x1 + a22x2 + … + a2nxn + a2n + 1 = 0 (3.1)
……………………………………
an1x1 + an2x2 + … + annxn + ann + 1 = 0
Левую часть каждого уравнения системы можно рассматривать как скалярное произведение двух векторов:
ai=(ai1, ai2, …, ain, ain+1)
x = (x1, x2, ..., xn, 1).
Таким образом, решение системы (3.1) сводится к построению вектора, ортогонального к каждому вектору ai. Добавим к системе векторов ai, линейно независимый от них вектор an+1 = (0, 0, ..., 0, 1). В векторном пространстве размерности n + 1 будем строить такой его ортонормированный базис
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.