Проект производства работ нулевого цикла на строительной площадке (размеры площадки - 400*500 м, место строительства - г. Новосибирск), страница 2

2 ОПРЕДЕЛЕНИЕ ОБЪЕМОВ ЗЕМЛЯНЫХ РАБОТ

2.1 Подготовка плана площадки

   Вершина левого верхнего угла прямо-угольной площадки находится на пересечении створа В по горизонтали и створа 1 по вертикали.  

   Для варианта №1 размер площадки задан 400x500 со стороной квадрата а = 100 м.

   Сетка квадратов наносится на плане участка для того, чтобы подсчет объемов
земляных работ вести по отдельным простейшим геометрическим фигурам. Размер стороны квадратов выбирают таким образом, чтобы в каждом из них проходило не более двух горизонталей и не менее одной.

   Определение объемов земляных работ можно производить и методом треугольников. Метод треугольников учитывает в определенной мере характер естественной поверхности в пределах каждого квадрата и поэтому дает более точные результаты. Каждый квадрат при этом методе разбивают на два треугольника диагональю, которая должна совпадать с направлением горизонталей. Если это условие нарушено, то погрешность в расчетах может оказаться большей, чем по методу квадратов.

Метод квадратов является более простым и для площадок со спокойным рельефом позволяет с достаточной точностью определить объемы. С увеличением сложности рельефа размер квадрата уменьшается.

   В данном случае рассмотрим метод квадратных призм.

   План площадки с нанесенной на него координатной сеткой квадратов вычерчивается на миллиметровке в масштабе 1:1000 или 1:2000. На горизонталях подписываются их абсолютные отметки, квадраты нумеруются. Проектный уклон принимается в направлении горизонтальной или вертикальной оси с учетом рельефа так, чтобы скат спланированной площадки был обеспечен с минимальными рабочими отметками при отсыпке насыпи или разработке выемки

   В вершинах квадратов подписываются рассчитанные черные (натурные), красные (проектные) и рабочие отметки.

2.2  Определение отметок и положения нулевой линии

2.2.1 Отметки поверхности земли

Отметки поверхности земли (черные или натурные) определяются в углах квадратов интерполяцией по кратчайшему расстоянию между соседними горизонталями с точностью до 0,01 м

Рис.2.1. Определение черных отметок методом интерполяции

Приращение отметки земли в рассматриваемой вершине квадрата по отношению к отметке горизонтали с меньшим значением:

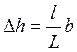                                              ,                                      (2.1)

где L — кратчайшее расстояние между соседними горизонталями, определяемое по масштабу, м; l — расстояние от вершины квадрата до горизонтали с меньшим значением, м; b— разница отметок соседних горизонталей, b = 1 м.

Черная отметка в вершине квадрата;

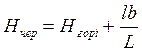,                                   (2.2)

где Н_гор — отметка горизонтали с меньшим значением, м.

   Отметка верхнего левого угла квадрата 18: для рассматриваемой точки измеренные на плане площадки расстояния оказались равны: L = 40 м, l = 5 м.

  Черная отметка в правой нижней вершине квадрата 6 равна:  

 Н_черн= 79+ (17∙1)/49=79,35 м.

   Рассчитанные   таким   образом   черные   отметки   всех   углов квадратов проставляются на плане площадки.

2.2.2 Проектные отметки

В курсовом проекте рассматриваются два возможных подхода к определению уровня планировки площадки: планировочный уровень определяется расчетом или планировка делается под заданную отметку.

   В первом случае плоскость спланированной площадки принимается с соблюдением нулевого баланса, т. е. когда планировка производится перераспределением земляных масс на самой площадке без завоза недостающего или вывоза избыточного грунта. Равенство выемки и насыпи обеспечивается, если планировочная отметка определена по величине средних черных отметок, взятых в углах квадратов. Во втором случае планировочная отметка задается преподавателем с учетом рельефа.

   Средняя   планировочная отметка   площадки   при   условии обеспечения нулевого баланса определяется по формуле:

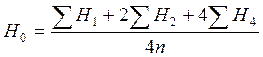                                     ,                                       (2.3)

где ∑Н₁ — сумма черных отметок точек, принадлежащих одному квадрату, м; ∑Н₂ — сумма черных отметок точек, где сходятся два угла квадратов, м; ∑Н₄ — сумма черных отметок точек, где сходятся четыре угла квадратов, м; n — количество квадратов.