Сборные железобетонные конструкции одноэтажного промышленного здания, страница 6

Сечение арматуры подбираем по усилиям в сечении 2-2, поскольку там дей­ствует наибольший по абсолютной величине момент М = 183 кН∙м при  N =958кН, (комбинация 1+3+7+15). В это сочетание входят усилия от длительно действующей нагрузки М_l=87 кН∙м при N_l=550 кН.

Так как в сочетание входят крановые нагрузки, расчетная длина надкрановой части колонны в плоскости изгиба: l₀=2H_в=2×4.05=8.1 м, а коэффициент условий работы бетона g_b2= 1,1.

Поскольку l₀/h_в= 7,7/0,6 =12,83>10, необходимо учитывать влияние прогиба элемента на величину эксцентрисите­та продольной силы.

Принимаем для колонны тяжелый бетон В20. По табл. 13 [2] R_b =11,5 МПа, R_bt = 0,9 МПа, с учетом g_b2= 1,1 R=1,1×11,5=12,65  МПа, R_bt=1,1×0,9=0,99 МПа. По табл. 18 [2] для бетона, подвергнутого тепловой обработке при атмосферном давлении, E_b= 24000 МПа.

Эксцентриситет продольной силы e₀=М/N=74/535=0,138м > e=h/30 =0,6/30 =0,02 м. Следовательно, случайный эксцентриситет не учитываем, так как колонна рамы – элемент статически неопре­делимой конструкции.

Найдем значение условной критической силы и величину коэффициента h для учета влияние прогиба элемента на величину эксцентриситета продольной силы. По п. 3.6 [2]

d_е=е₀/h=0,138/0,6=0,23 < d_e,min=0,5– 0,01∙ l₀/h– 0,01R_b=0,5– 0,01×7,7/0,6– 0,01×12,65= 0,245.

 Принимаем d_е = 0,245.

По п. 3.24 [2] определяем моменты относительно центра тяжести арматуры А_s:

 М = М + N ((h/2) – а) и M_l= ± М_l + N_l ((h / 2) – а).

М =74 +535× (0,5× 0,6 – 0,03) =218,45 кН∙м;

М_l =6 + 535× (0,5× 0,6 – 0,03) =150,45 кН∙м.

Тогда по п. 3.6 [2] j_l=1+bМ_l/М=1 + 150,45/218,45=1,69.

По п. 3.24 [2] условная критическая сила

.

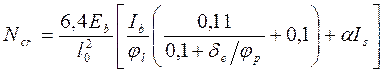В первом приближении принимаем  m= (А_s + А_s^’)/bh₀ = 0,005.

Тогда

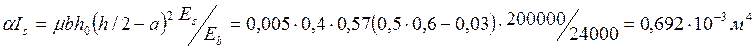
I_b=0,4×0,6³/12=7,2×10^-3 м⁴.

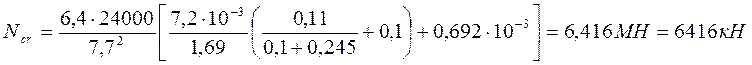
Коэффициент для учета влияние прогиба элемента на величину эксцентриситета продольной силы

h=1/(1 – N/N_cr)=1/ (1 – 535/6416) =1,091.

Тогда эксцентриситет продольной силы относительно центра тяжести арматуры А_s

е=е₀ η+ (h₀ – а')/2= 0,138×1,091 + (0,57 – 0,03) /2 =0,421 м.

Относительная величина продольной силы

a_n=N/R_bbh₀²=535×10^-3/(12,65×0,4×0,57²)=0,185< x_R=0,581.

Здесь x_R находим при g_b= 1,1. Далее вычисляем коэффициенты

a_m1=Nе/R_bbh₀= 535×10^-3×0,421/(12,65×0,4×0, 57)=0,137 и d=a'/h₀=0,03/0,57=0,0526

Тогда требуемая площадь арматуры

 

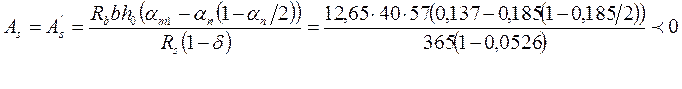
По расчету арматура не требуется принимаем ее конструктивно по 2Æ12 А –III с каждой стороны колонны (А_s=A_s'=2,26см²). Принятая арматура обеспечивает m = 4,52×100/(40∙57) = 0,2 %, что равно m_min=0,2 %.

Расчёт из плоскости изгиба.

За высоту сечения принимаем размер из плоскости изгиба, h = b = 0,4 м. Расчетная длина надкрановой части колонны из плоскости изгиба   l₀= 1,5Н_в= 1,5 × 3,85= 5,775 м. Поскольку l₀/h=14,4 , а усилие приложено со случайным эксцентрисите­том, поверку прочности из плоскости изгиба не делаем.

3.1.2 Подкрановая часть колонны

Размеры прямоугольного сечения подкрановой части: b= 400 мм, h_H = 700 мм. Для продольной арматуры принимаем а = а' = 30мм. Тогда рабочая высота сечения h₀= 0,7 - 0,03 = 0,67 м.

Расчет в плоскости изгиба. Сечение арматуры подбираем по усилиям в сечении 4-4, поскольку там действу­ет наибольший по абсолютной величине момент М = -126 кН∙м при

N = 725 кН (комбинация 1+14). В это сочетание входят усилия от длительно действующей нагрузки M_l= - 56 кН-м при  N_l= 725 кН.

Так как в сочетание входят крановые нагрузки, расчетная длина надкрановой части колонны в плоскости изгиба по табл. 32[ 2 ]: l₀=1,5∙H_H = 1,5∙(9,75-3,85) = 8,85 м, а коэффициент условий работы бетона γ_b2= 1.1.

Поскольку l₀/h_н= 8,85/0,7 =12,64>10, необходимо учитывать влияние прогиба элемента на величину эксцентрисите­та продольной силы.

Эксцентриситет продольной силы e₀=М/N=126/725=0,174 м > e=h/30 =0,7/30 =0,023 м. Следовательно, случайный эксцентриситет не учитываем, так как колонна рамы – элемент статически неопре­делимой конструкции.

Найдем значение условной критической силы и величину коэффициента h для учета влияние прогиба элемента на величину эксцентриситета продольной силы. По п. 3.6 [2]