Экспериментальное исследование статического и астатического регулирования линейной системы автоматического регулирования

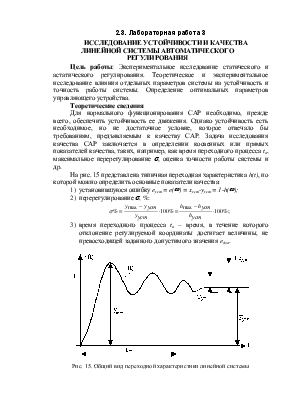
Исходя из выражений (14) и (15), получим значение оптимального суммарного коэффициента передачи интегрирующего блока. При использовании ПИ-регулятора он равен:

.

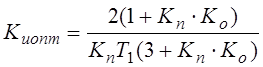Для И-регулятора оптимальный коэффициент передачи интегрирующего блока равен:

.

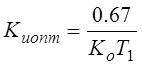Практическое задание:

1.  Рассчитать область возможных значений коэффициента K_u, при котором выполняется условие устойчивости САР. Расчет выполнить отдельно для И и ПИ-регуляторов с учетом приведенных в табл. 3 и 4 параметров (формулы 4 и 3, K_u = 1/T_u).

2.  Рассчитать оптимальные значения коэффициента K_u для И и ПИ-регуляторов.

3.  В VisSim собрать структурную схему системы согласно варианту (табл. 3, 4, рис. 17).

4.  Рассчитать передаточную функцию замкнутой системы с ПИ-регулятором используя оптимальное значение K_u для ПИ-регулятора.

5.  Рассчитать передаточную функцию замкнутой системы с И-регулятором используя оптимальное значение K_u для И-регулятора.

6.  Проверить экспериментально выполнение условий устойчивости для И и ПИ-регуляторов при K_u взятом из области устойчивости.

7.  Проверить экспериментально выполнение условий устойчивости для И и ПИ-регуляторов при K_u = K_uопт.

8.  Для САР с И и ПИ-регулятором экспериментально исследовать переходной процесс при различных значениях K_u.

9.  Проверить систему на устойчивость и построить график расположения корней (файл «уст_мат_признак»), найти критический коэффициент усиления системы (файл «уст_Гурвиц»).

10.  Построить годограф Михайлова (файл «уст_Михайлов»).

11.  Для САР с П-регулятором в Mathcad рассчитать установившуюся ошибку . Построить график зависимости .

12.  Для САР с И и ПИ-регулятором в Mathcad определить зависимость интегральной оценки от K_u. Построить график зависимости .

 Методика выполнения работы:

1.  Запустите программу VisSim щелчком на ярлыке программы на рабочем столе.

2.  Соберите структурную схему системы согласно варианту. Задайте параметры передаточной функции объекта (табл. 3).

3.  В передаточной функции регулятора задайте передаточную функцию И-регулятора  с K_u взятым из рассчитанной области допустимых значений. Проведите моделирование.

4.  Задайте следующие значения K_u:

Проведите моделирование и для каждого полученного переходного процесса рассчитайте величину перерегулирования (s, %) и время переходного процесса (t_п, с).

5.  Повторите п.3-4 для ПИ-регулятора.

6.  Откройте файл уст_мат_признак. Введите коэффициенты передаточной функции замкнутой системы с ПИ-регулятором. Проведите моделирование.

7.  Постройте график корней. Для этого выделите блок . Нажмите левую кнопку мыши на свободном поле диаграммы выше и левее этого блока. Тяните указатель мыши вправо и вниз. Блок будет выделен. Выберите команду Root Locus в меню Analyze. В правом нижнем углу диаграммы появится график расположения корней системы. Сделайте выводы об устойчивости. Для устойчивой системы по расположению корней определите степень устойчивости (a).

8.  Постройте годограф Найквиста. Выделите блоки передаточных функций и выберите команду Nyquist Response в меню Analyze. Появится годограф Найквиста. Обратите внимание, в VisSim годограф Найквиста строится при изменении частоты от -¥ до +¥, в отличие от классического метода ТАУ, когда частота изменяется от 0 до +¥.

9.  Откройте файл уст_Гурвиц. Задайте коэффициенты передаточной функции замкнутого контура. Проведите моделирование. По графику переходного процесса и по блокам Light (raz Opred [n]) определите устойчивость системы. Система устойчива только при положительных определителях Гурвица.

10. Откройте файл уст_Михайлов. Задайте коэффициенты передаточной функции замкнутого контура. Проведите моделирование. По годографу Михайлова и по переходному процессу определите устойчивость системы. По годографу Михайлова определите запас устойчивости. Для этого измените масштаб графика с годографом Михайлова.

11. Запустите программу Mathcad щелчком на ярлыке программы на рабочем столе.

12. Для исследования зависимости установившейся ошибки  от K_п для П-регулятора задайте постоянным коэффициент K_о, а K_п задайте от 0.05 до 1 с шагом 0,01, задайте в виде функциональной зависимости (см. теорию). Постройте график.

13. Для построения зависимости  для И-регулятора значение K_u должно изменяться в пределах области допустимых значений для И-регулятора. Значение интегральной квадратичной оценки задайте в виде функциональной зависимости от K_u (см. теорию). Постройте график.

14. Повторите п.13 для ПИ-регулятора.

ВАРИАНТЫ ПРАКТИЧЕСКОГО ЗАДАНИЯ

Таблица 3

Таблица 4

Содержание отчета:

Для защиты лабораторной работы необходим отчет с расчетами в рукописном виде и распечатанными (либо перерисованными) графиками. Все используемые файлы необходимо сохранять под другим именем в своей папке.

1.  Титульный лист.

2.  Расчет области допустимых значений K_u для И и ПИ-регуляторов.

3.  Расчет оптимальных значений K_u для И и ПИ-регуляторов.

4.  Расчет передаточной функции замкнутой системы с ПИ-регулятором с оптимальным значением K_u.

5.  Схема системы собранная в VisSim.

6.  Графики переходных процессов для И-регулятора при,,. Для каждого переходного процесса расчет перерегулирования (s, %) и времени переходного процесса (t_п, с).

7.  Графики переходных процессов для ПИ-регулятора при,,. Для каждого переходного процесса расчет перерегулирования (s, %) и времени переходного процесса (t_п, с).

8.  График корней и годограф Найквиста.

9.  Годограф Михайлова и значения запаса устойчивости.

10.   Для П-регулятора график зависимости из Mathcad.

11.   Для И и ПИ-регуляторов графики зависимости  из Mathcad.

12.   Вывод.

Контрольные вопросы:

1.  Дать определение статической и астатической систем.

2.  Объяснить влияние типа регулятора на устойчивость и ошибку системы.

3.  Оценки качества процесса регулирования.

4.  Дать определение и физическую трактовку понятия «устойчивая система».

5.  Дать формулировку критериев устойчивости: Гурвица, Михайлова, Найквиста, логарифмического критерия.

6.  Как влияет передаточный коэффициент разомкнутого контура системы на ее устойчивость в замкнутом состоянии?

7.  По какой динамической характеристике системы и как оценивают