Интегральные оценки качества

Интегральные оценки качества

Каждый из прямых показателей качества характеризует только одно какое-либо свойство системы или качество переходного процесса или частотной характеристики.

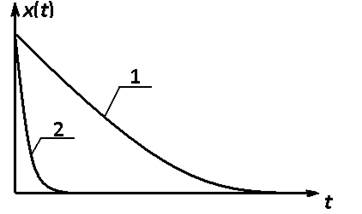С точки зрения качества процесса регулирования, 2-й процесс лучше, т.к. затухание происходит быстрее и время переходного процесса меньше t_р2 <t_р1. Соответственно, площадь, ограниченная кривой переходного процесса, меньше и меньше время переходного процесса. Математически площадь, ограниченная кривой, определяется интегралом.

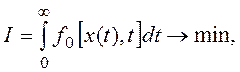
Интегральные оценки представляют собой определенные интегралы во времени от 0 до бесконечности

где х(t) – регулируемая или управляемая величина, либо сигнал ошибки e(t).

Здесь, пределы от 0 до  ¥, т.к. реально любой переходной процесс в системе заканчивается за бесконечно большое время.

Подынтегральная функция f₀ выбирается таким образом, чтобы интеграл характеризовал качество системы и выражался через коэффициент передаточной функции замкнутой системы. Этот интеграл должен быть сходящимся, поэтому в функцию f₀ входят не абсолютные значения x(t) или e(t), а их отклонения от конечных установившихся значений.

Первая интегральная оценка, является более простой.

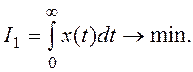Первая интегральная оценка I₁ определяется интегралом

Чем меньше I₁, тем качество процесса регулирования лучше, так как площадь, ограниченная кривой меньше.

На практике I₁ вычисляют по выражению:

,

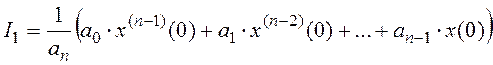здесь а₀, а₁,…, а_n – коэффициенты характеристического уравнения;

 х(0), х^’(0),…, х^(n-1)(0) – начальные условия для уравнения n-го порядка.

При исследовании систем и решении задач синтеза одноразовые вычисления интегральных оценок положительного результата не дают. Необходимо выполнить ряд вычислений при  разных значениях параметров, которые дают глобальный минимум интегральных оценок. Первая интегральная оценка применяется для монотонного процесса и процесса без перерегулирования. Вид переходного процесса можно определить либо построив h(t), либо для систем третьего порядка воспользоваться диаграммой Вышнеградского.

Вторая интегральная оценка

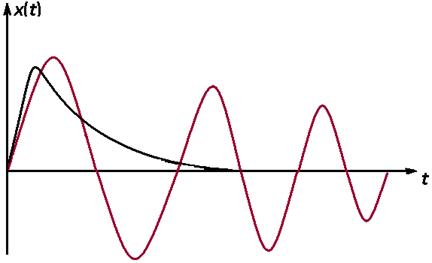Если процесс колебательный или с перерегулированием, то первой интегральной оценки пользоваться категорически нельзя, так как результат будет заведомо ложный, т.к. х(t)-знакопеременная функция.

Если воспользоваться оценкой I₁, то мы получим очень малое значение этой оценки при неудовлетворительном качестве, так как  положительные области компенсируют отрицательные.

В результате интеграл стремится к минимуму, хотя качество процесса значительно хуже.

Вторая интегральная оценка учитывает все участки кривой x(t):

 

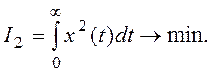На практике вторая интегральная оценка вычисляется по уравнениям, приведенным в справочной литературе, по коэффициентам полиномов числителя и знаменателя передаточной функции

 

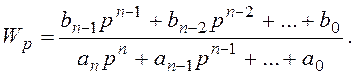Например:

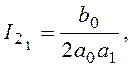при n=1         

 

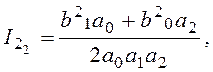при n=2            

где m - степень полинома числителя n - степени полинома знаменателя

Вторая интегральная оценка I₂ более представительна, она учитывает не только знаменатель передаточной функции но и коэффициенты числителя.

Одноразовое вычисление I₂ положительных результатов не дает, необходимо произвести ряд вычислений и выбрать те параметры, при которых I₂ будет иметь глобальный минимум. При этих значениях параметров качество процесса регулирования наилучшее.

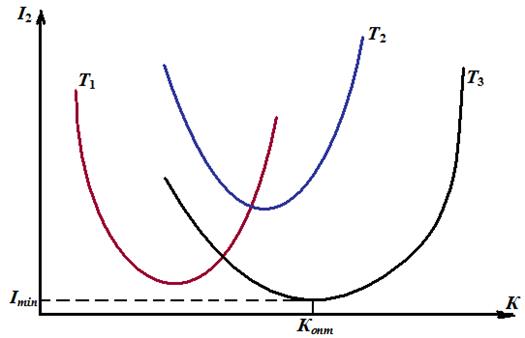
Например, на рисунке варьировали параметрами К и Т для одной и той же системы. Глобальный минимум наблюдается при Т₃ и некотором значении К, назовем его оптимальным, т.к. при минимуме I₃ качество процесса регулирования наилучшее.

Это пассивный поиск экстремума. Глобальный минимум (экстремум) можно найти, используя активный метод, то есть составляется система двух уравнений (частных производных интегральной оценки)

 

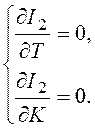Решая эту систему, находят значения K_i и T_i, которые дают глобальный минимум интегральной оценки.

Оценка I₂ лишена недостатков первой интегральной оценки, но все-таки имеет недостатки: I₂ не учитывает скорость затухания процесса. Этот недостаток учитывается в третьей интегральной оценке.

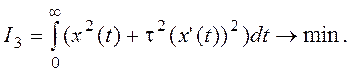Третья интегральная оценка определяется интегралом

Одноразовое вычисление I₃ положительного результата также не дает, необходим ряд вычислений.