2.1.8.3.1. Эллипсоид. Так
называется поверхность, каноническое уравнение которой 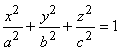 .
В координатной плоскости z = 0 (т.е. в.плоскости
Оху) след этой поверхности есть эллипс
.
В координатной плоскости z = 0 (т.е. в.плоскости
Оху) след этой поверхности есть эллипс 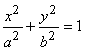 ,
в плоскости у = 0 получаем эллипс
,
в плоскости у = 0 получаем эллипс 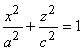 ,
в плоскости х = 0 - эллипс
,
в плоскости х = 0 - эллипс 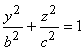 . Поверхность
изображена на картинке справа. В случае, когда две полуоси эллипсоида равны, эллипсоид
будет являться поверхностью вращения; так, если
. Поверхность
изображена на картинке справа. В случае, когда две полуоси эллипсоида равны, эллипсоид
будет являться поверхностью вращения; так, если
а = с, то эллипсоид 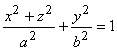 может
быть получен в результате вращения эллипса
может
быть получен в результате вращения эллипса 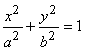 вокруг
оси Оу.
вокруг
оси Оу.
 2.1.8.3.2. Конус. Так
называется поверхность, каноническое уравнение которой
2.1.8.3.2. Конус. Так
называется поверхность, каноническое уравнение которой 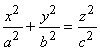 .
В плоскости z = 0 получаем
.
В плоскости z = 0 получаем 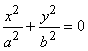 ; единственная точка, удовлетворяющая
этому уравнению – точка
; единственная точка, удовлетворяющая
этому уравнению – точка 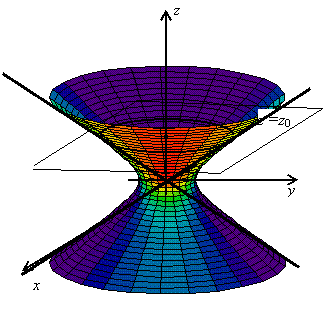 О(0, 0). В плоскости у
= 0 получаем
О(0, 0). В плоскости у
= 0 получаем 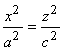 , это уравнение пары прямых
, это уравнение пары прямых
![]() . В плоскости х = 0 уравнение
. В плоскости х = 0 уравнение 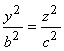 даст пару прямых
даст пару прямых ![]() . В плоскостях z
=
. В плоскостях z
= ![]() z0
получаем
z0
получаем 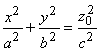 , или
, или 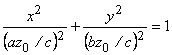 ,
это уравнения эллипса с полуосями (az0/c) и (bz0/c), линейно расширяющимися с ростом z0.
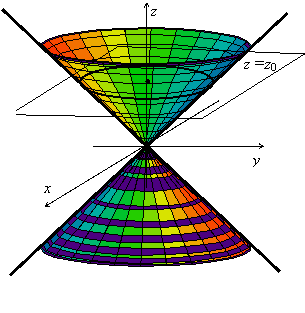
Поверхность изображена на картинке справа. Если а = b,
поверхность будет конусом вращения.
,
это уравнения эллипса с полуосями (az0/c) и (bz0/c), линейно расширяющимися с ростом z0.
Поверхность изображена на картинке справа. Если а = b,
поверхность будет конусом вращения.
2.1.8.3.3. Однополостный
гиперболоид. Эта поверхность имеет каноническое уравнение 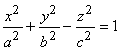 . Уравнение пересечения этой
поверхности с плоскостью z = 0 - эллипс
. Уравнение пересечения этой
поверхности с плоскостью z = 0 - эллипс 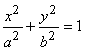 с полуосями a и b. В плоскостях
с полуосями a и b. В плоскостях
х = 0 и у = 0 получаем гиперболы 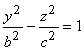 и
и 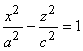 с
мнимой осью Oz, в сечениях поверхности
плоскостями z =
с
мнимой осью Oz, в сечениях поверхности
плоскостями z = ![]() z0 получаем эллипсы
z0 получаем эллипсы 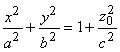 ,
вершины которых находятся как раз на гиперболах в плоскостях х = 0 и
,
вершины которых находятся как раз на гиперболах в плоскостях х = 0 и
у = 0. Поверхность изображена на картинке справа.
 2.1.8.3.4. Двуполостный гиперболоид. Эта
поверхность имеет каноническое уравнение
2.1.8.3.4. Двуполостный гиперболоид. Эта
поверхность имеет каноническое уравнение 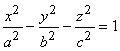 .
Так как
.
Так как 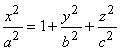 , то
, то ![]() . В
плоскостях у = 0 и z = 0 получаем гиперболы
с действительной осью Ох, сечение поверхности плоскостями х =
. В
плоскостях у = 0 и z = 0 получаем гиперболы
с действительной осью Ох, сечение поверхности плоскостями х = ![]() х0 (х0
> a) дает эллипсы
х0 (х0
> a) дает эллипсы 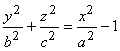 .
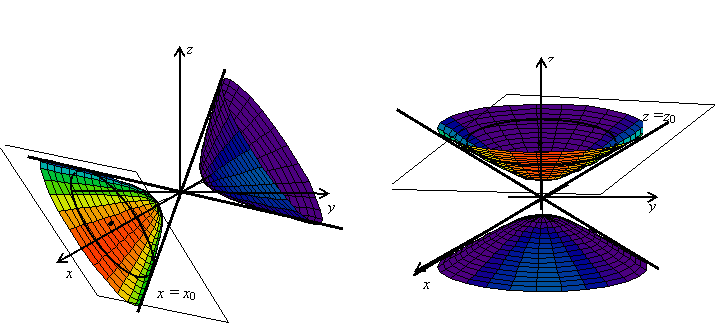
Поверхность изображена на рисунке слева. В случае, когда действительной осью
является ось Oz, поверхность имеет уравнение
.
Поверхность изображена на рисунке слева. В случае, когда действительной осью
является ось Oz, поверхность имеет уравнение 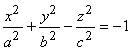 (рисунок справа).
(рисунок справа).
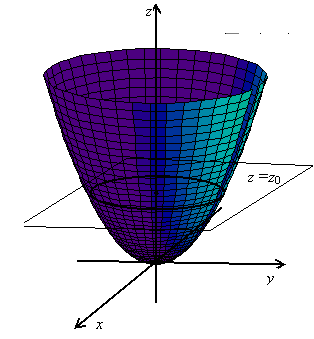 2.1.8.3.5. Эллиптический параболоид. Эта
поверхность задается каноническим уравненим
2.1.8.3.5. Эллиптический параболоид. Эта
поверхность задается каноническим уравненим 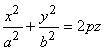 .
В плоскостях х = 0 и у = 0 получаются параболы
.
В плоскостях х = 0 и у = 0 получаются параболы 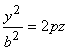 и
и 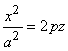 ,
в сечении
,
в сечении
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.